フーリエ変換のイメージと数式の意味をわかりやすく説明したい（複素数verも）

本記事では、フーリエ変換のイメージと数式の意味についてわかりやすく解説できたらなと思います。 より理解しやすいフーリエ級数展開 / フーリエ係数を中心として話を進めていきますが、フーリエ逆変換 / フーリエ変換もイメージはほとんど同じです。 違いは、元の波形（関数）$f(t)$ が周期関数であるかどうかだけで、これによって数式も少し異なります。 以下の周期関数の式は、周期 $T$ の場合の式になります。

• $f(t)$ : 時間 $t$ の波形、関数
• $t$ : 時間
• $T$ : 周期関数の繰り返し周期
• $\nu$ : 周波数

フーリエ変換とは

フーリエ変換のイメージ：分解後の各成分の大きさを求める

フーリエ変換を一言で言うと、ある波形にどの周波数のcos (sin) 成分がどれだけ多く含まれているか、を求めることです。 あらゆる波形（関数）は、周波数の異なる多数の三角関数（cosとsin）を足し合わせた形に分解できます。このときのそれぞれのcos, sinの大きさを求める演算がフーリエ変換（フーリエ係数の算出）になります (Fig.1) 。

下のグラフでは、足し合わせるcosとsinそれぞれの大きさを操作することができ、足し合わせた後の波を左下に、それをフーリエ変換したものが右下のグラフになります。

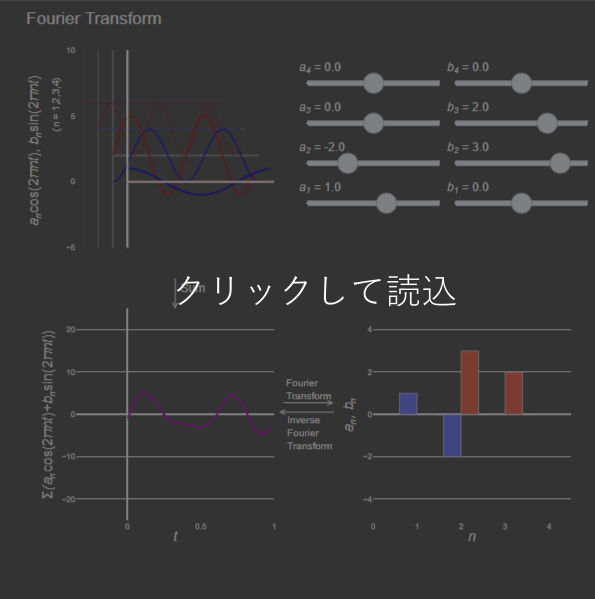
元の波が時間の関数であれば、フーリエ変換後は周波数（角周波数、周期）ごとの大きさ、つまり周波数（角周波数、周期）の関数となります。”スペクトル”とよく呼ばれるのはこれに該当します。一方で、元の波が空間（位置）の関数であれば、フーリエ変換後は波長（波数）の関数になります。 つまり時間に関する波形か空間に関する波形かによって、変換パラメーターの次元（単位）が異なるということです。 時間・空間に関する波のパラメーターに関してはこちらで述べています。

cosのみ（sinのみ）での表現

波を表現するときにcosとsinの両方を使わず、cosのみ（またはsinのみ）で表現することもできます。 そのときは、sin (またはcos) が消えることになりますが、初期位相（位相差）$\phi$ という変数が1つ加わることになります。 つまり下の2つの式は、表現の形式が異なるだけで、同じ波を意味します。

cosの大きさ $a$ とsinの大きさ $b$ の2つによって、cos単体の大きさ（振幅）$a’$ とその初期位相 $\phi$ を表現しているというわけですね。 2つの式の変換は、三角関数の加法定理

$$\cos (\alpha + \beta) = \cos\alpha\cos\beta -\sin\alpha\sin\beta$$

を使うことで実行でき、

$$\begin{aligned} a’\cos (2\pi f + \phi) & = a’\cos(2\pi f) \cos\phi-a’\sin(2\pi f )\sin\phi\\ & = a\ \cos(2\pi f) +b\ \sin(2\pi f ) \end{aligned}$$

となります（ここで、$a=a’\cos\phi$, $b=-a’\sin\phi$）。

フーリエ変換は、元の波形に周波数の異なるcosとsinがそれぞれどれだけ含まれるかを算出しているわけですから、言い換えれば、元の波形に含まれるcosの振幅と初期位相を周波数ごとに求めていることに相当します。

複素数を使ったコンパクトな表現

フーリエ変換の式には、複素数を使った表現がよく使われています。この複素数はcosとsinを別の形で表したものです。この表現を使うと最終的な数式が簡潔にまとめられます。ある波形（関数）$f(t)$ をcos・sinの和で表した式と複素数で表した式（フーリエ級数展開）をそれぞれ下に示します。

• cosとsinを使った形式：$\displaystyle f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty}\left\{a_n \cos\left(\frac{2\pi nt}{T}\right) + b_n \sin\left(\frac{2\pi nt}{T}\right)\right\}$
• 複素数を使った形式：$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}c_n e^{i2\pi nt/T}$

複素数を使った形式の方が短くコンパクトになっているのが分かります。

cosとsinを使った表現から複素数を使った表現に変換するときには、オイラーの公式を使います (Fig.2) 。オイラーの公式を変形すると

$$\displaystyle \cos\theta = \frac{e^{i\theta}+e^{-i\theta}}{2},\ \ \sin\theta = i\frac{-e^{i\theta}+e^{-i\theta}}{2}$$

のようにcosとsinを複素数の形に書き換えられるので、これをそのまま代入してまとめていけば、フーリエ変換の式をコンパクトにまとめることができます。

なぜ成分分解できるのか

あらゆる波が多数の複素数（またはcos, sin）の和で表せますが、なぜフーリエ変換の式を使うと足し合わせる前のそれぞれの成分の大きさ（係数）を抽出できるのでしょうか。この原理はベクトルの各成分の大きさを求める過程ととても似ています。

基本成分が直交（線形独立）していると抽出できる

ある波形（関数）からそれを構成している成分の係数を抽出できるのは、基本成分が直交（線形独立）しているためです。まずはベクトルの場合から考えてみましょう。

ベクトルのとき

$x, y, z$ 方向それぞれの基底ベクトルを $\boldsymbol{i}, \boldsymbol{j}, \boldsymbol{k}$ としたときに、これらの成分の大きさがそれぞれ $a_x, a_y, a_z$ であるベクトル $\boldsymbol{a}$ を考えます。以下のようにそれぞれの成分の和の形でベクトルを表すことができます。

$$ \boldsymbol{a} = a_x\boldsymbol{i}+a_y\boldsymbol{j}+a_z\boldsymbol{k} $$

このベクトルを構成する成分それぞれの大きさ（係数$a_x, a_y, a_z$​ ）を計算で求めるにはどうすればよいでしょうか。答えは、大きさを求めたい成分（基底ベクトル）と元のベクトルの内積を取る、です（Fig.3）。 たとえば $\boldsymbol{i}$ ベクトル（xx方向）成分の大きさ $a_x$ を求めたければ、$\boldsymbol{a}$ と $\boldsymbol{i}$ の内積をとって

$$\boldsymbol{a}\cdot\boldsymbol{i} = a_x\boldsymbol{i}\cdot\boldsymbol{i}+a_y\boldsymbol{j}\cdot\boldsymbol{i}+a_z\boldsymbol{k}\cdot\boldsymbol{i}=a_x$$

のように求めることができます。 なぜこのように内積を取ると、各成分の大きさを求められるかというと、求めたい成分以外は内積を取ったときに=0で消えるためです（Fig.3右）。 他の基本成分同士の内積がゼロになるときのこと「直交している」といいますが、この性質が非常に役立っているということになります。 内積の値は内積をとったもの同士がどれだけ類似しているかを示す相関のようなものを意味しますので、基底ベクトルの内積がゼロ、つまり基本成分同士がまったく似ていない（線形独立している）からこそ、各成分ごとに分離することができると言えるでしょう。

波形（関数）のとき　～基本成分 : cos, sin～

関数のときでも、ベクトルと同じように考えて、構成成分の大きさを算出できます。 これがフーリエ変換（フーリエ係数の算出）の原理です。 ある波形 $f(x)$ は、無限個のcos, sinを基本成分とした和で表すことができ（フーリエ級数展開）

$$\displaystyle f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty}\left\{a_n \cos\left(\frac{2\pi nt}{T}\right) + b_n \sin\left(\frac{2\pi nt}{T}\right)\right\}$$

となります。このそれぞれのcos, sinの大きさ（係数 $a_n, b_n$ ) を求めたいのですが、このとき使うのが「関数の内積」です。

関数 $f(x), g(x)$ の内積 : $\displaystyle <f(x), g(x)> = \int_{-\infty}^{\infty} f(x)\cdot g(x) dx$

この演算がなぜ内積になるのか、については後で説明しますが、元の波形 $f(t)$ と基本成分 $\cos(2\pi nt/T)$, $\sin(2\pi nt/T)$ $_{(n=0,1,2,\cdots)}$ の内積をとることで、その基本成分の大きさ（係数）を求めることができます (Fig.4) 。 内積の定義では、積分範囲が $-\infty$ から $\infty$ となっていますが、フーリエ係数を算出する場合には被積分関数 $f(x)\cdot g(x)$ が周期関数になるため、積分範囲を1周期分だけに単純化しています。 基本成分であるcos, sinの大きさ（フーリエ係数）を求めるときもベクトルのときと同様に、他の基本成分同士の内積を取るとゼロになる（直交している）という性質がカギになります。 基本成分の$\cos(2\pi nt/T)$, $\sin(2\pi nt/T)$ $_{(n=0,1,2,…)}$​ 同士が直交していることは計算（三角関数の積和公式を使用）で確かめられます。 他の基本成分同士が直交しているので、基本成分の1つと元の波形の内積をとると、他の基本成分が消えることとなり、基本成分の大きさ（係数）1つだけを抽出できます（Fig.4) 。

波形（関数）のとき　～基本成分 : 複素数（指数）～

複素数（指数）関数のときもcos, sinのときと同じようにして、構成成分の大きさ（係数）を算出することができ、これがフーリエ変換（フーリエ係数の算出）になります。 ある波形 $f(t)$ は、無限個の複素数（指数）を基本成分とした和で表すことができ（フーリエ級数展開）

$$ \displaystyle f(t) = \sum_{n=-\infty}^{\infty}c_n e^{i2\pi nt/T}$$

となります。このそれぞれの指数の大きさ（係数 $c_n$ ）を求めたいので、以下のような「関数の内積」を使います。

複素関数 $f(x), g(x)$ の内積 : $\displaystyle <f(x), g(x)> = \int_{-\infty}^{\infty} f(x)\cdot g(x)^* dx$

ここでの $g(x)^*$は $g(x)$ の複素共役（虚部の符号を反転させたもの）です。 このようにcos, sinのときとは内積の定義が少し異なり、複素関数の内積では複素共役をとる必要がでてくるので注意が必要です。 関数の内積については後にも述べます。 基本成分 $\displaystyle e^{i2\pi nt/T}$ $_{(n=0,1,2,…)}$ 同士で内積をとると、$n$ が異なる場合ゼロになる、つまり基本成分はそれぞれ直交しているので、基本成分がcos, sinのときと同様にフーリエ級数展開したときのそれぞれの係数 $c_n$ を求めることができます (Fig.5) 。 元の波形（関数）$f(x)$ と、基本成分の1つと内積をとると、展開したあとの $f(x)$ はその基本成分以外の項がゼロで消えるため、基本成分の大きさ（係数）1つだけを抽出できます。

数式の意味：関数の内積

フーリエ係数の算出（フーリエ変換）では、関数の内積を使っていることを述べました。 ここで、なぜ関数の内積がこのような数式の形になるのか、ベクトルと比較して説明しようと思います。

ベクトルの内積は、各成分同士をかけ合わせた総和です。 この値がゼロのときはベクトル同士が直交している、つまり両者は似ていない（相関がない）というようなことを意味します。

関数の場合、$f(-\infty)\cdots ,f(-1), f(0), f(1),\cdots f(\infty)$ それぞれを関数の構成成分と考え、$\infty$ 次元ベクトルのように捉えることで内積を定義しています。 そのため関数の内積は、構成成分 $f(-\infty)\cdots$, $f(-1)$, $f(0)$, $f(1),\cdots f(\infty)$ と $g(-\infty)\cdots$ ,$g(-1)$, $g(0)$, $g(1),\cdots g(\infty)$ 同士で積をとり、その総和を算出しているわけです。 一般的な関数 $f(x)$ は、$x$ の値が連続的に存在する（たとえば $f(0)$ と $f(1)$ の間にも $f(0.5)$, $f(0.50000001\cdots)$ など無限に存在する）ので、積分という形で総和をとっています。

複素関数の内積では、一方の関数は複素共役（虚部の符号を反転）をとります。

複素共役をとらないと、自身との内積が（$i^2=-1$なので）負になる可能性が出てきてしまうため、複素関数での内積では複素共役をとる必要がでてきます。 自身との内積 = 自身の大きさの2乗（ベクトル $\boldsymbol{a}$ の場合、$\boldsymbol{a}\cdot\boldsymbol{a} = |a|^2$ ）であり、本来、負にはならないはずなのでこうしないと整合性がとれないという事情からこのような形になります。

まとめ

• あらゆる波形（関数）は、三角関数（cosとsin）の和で表せる（フーリエ級数展開、フーリエ逆変換）
• cos, sinの代わりに複素数を使うとコンパクトになる
• フーリエ係数の算出（フーリエ変換）では、元の関数と基本成分（cos, sin）との内積を求めている
• 基本成分（周波数の異なるcos, sin）はそれぞれ直交しているため、基本成分1つだけの大きさ（係数）を算出できる