【plotly】偏光板、波長板を回転したときの偏波をグリグリしてみる
投稿日:2020年7月16日 更新日:
内容
インタラクティブなグラフで偏波の挙動を表現し、回転させたときの偏光板, 波長板の働きをみてみる。
動機
最近、偏光板や波長板を回転させて偏波を変化させる偏波コントローラを触る機会がありました。偏光板は直線偏光を一方向に切り出し、λ/2波長板は直線偏光の角度を変え、λ/4波長板は直線偏光を円偏光にする働きをするのは知っていましたが、それらを回転させたときに何が起こっているのかしっくりこなかったので、pythonのグラフ化ライブラリのplotlyでインタラクティブなグラフを作成して、簡単に偏波の動きを確認してみました。グラフのパラメータを変えたり、グリグリと視点を動かしたりしてみると、何となくつかめたものがある気がします。plotlyのグラフ自体は、以前の記事で作成したグラフに手を加えて作成しました。初めに光学素子を回転させたグラフを作成してみましたが光学素子の働きが把握しづらいと感じたため、光学素子は固定して入射光を回転させるグラフも作成しています(両者は視点が違うだけで、偏波の動きは同じ)。
偏光板, 波長板を透過した偏光をみてみる
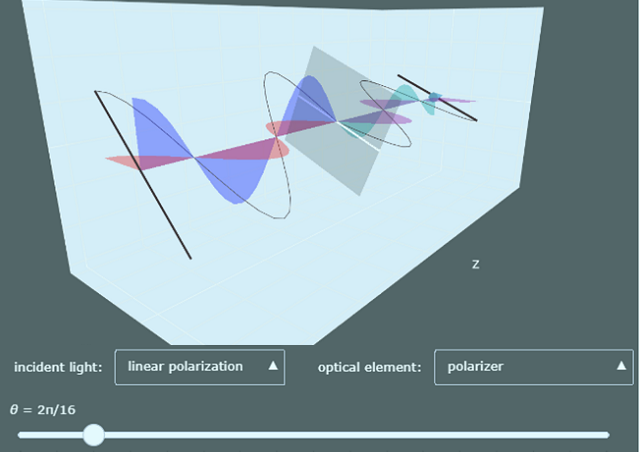
プロット1 :光学素子の回転
スライダーを左右に動かすと、光学素子を回転させることができます。
プロットしているもの
光はz軸方向に直進しており、入射した光が光学素子(偏光板 or λ/2波長板 or λ/4波長板)に入り、偏波が操作されて透過している様子をプロットしています。グラフでは、以下のものがプロットされています。
- 黒線(細):入射光および透過光の偏波
- 黒線(太):zを固定したとき(x-y平面)での偏波の動き
- 赤色の平面:入射光の偏波のx軸方向成
- 青色の平面:入射光の偏波のy軸方向成分
- 紫色の平面:透過光の偏波のx軸方向成分
- 水色の平面:透過光の偏波のy軸方向成分
- 灰色の正方形:光学素子(偏光板 or λ/2波長板 or λ/4波長板)、白線が偏光板の偏光軸または波長板のファスト軸を示す
- プルダウン, スライダーによる操作
- “incident light”プルダウン:入射光の偏光を直線, 楕円, 円に切り替えられる
- “optical element”プルダウン:光を透過させる光学素子を波長板, λ/2波長板, λ/4波長板の中から選択できる
- スライダー:偏光板の偏光軸(または波長板のファスト軸)の角度Θを動かすことができる(Θ:x軸と偏光軸 or ファスト軸のなす角)
ソースコード
【表示する】
#!/usr/bin/env python
# -*- coding: utf-8 -*-
#%% モジュールのインポート
import plotly.graph_objects as go
import plotly.offline as py
import numpy as np
py.init_notebook_mode(connected = True)
#%% パラメータ設定
PI = np.pi
THETA_OPT_ELEM = 0 # 光学素子の角度
DROP_DECIMALS = 3 # 出力値の桁数
#%% ジョーンズマトリックス計算
class CalcJVecs:
def __init__(self):
self.__make_jmat_list()
self.__make_in_jvec_list()
self.__operate_rotate_mat()
# 入射光のジョーンズベクトル
def __make_in_jvec_list(self):
jvec_liner = [1,1] / np.sqrt(2) # 直線偏波
jvec_ellipt= [np.exp(1.j*PI/5),1] / np.sqrt(2) # 楕円偏波
jvec_circul= [1.j,1] / np.sqrt(2) # 円偏波
jvec_in_list = np.array([jvec_liner, jvec_ellipt, jvec_circul])
#self.jvec_in_list = jvec_in_list
self.jvecs_in = jvec_in_list[np.newaxis,:,np.newaxis,:]
self.jvec_num = jvec_in_list.shape[0]
# 光学素子のジョーンズマトリックス
def __make_jmat_list(self):
jmat_pol = [[1,0],[0,0]] # 偏光板
jmat_hwp = [[1,0],[0,-1]] # ラムダ/2 波長板
jmat_qwp = [[1,0],[0,1.j]] # ラムダ/4 波長板
#jmat_list = np.array([jmat_pol, jmat_hwp, jmat_qwp ])
jmat_list = np.array([jmat_pol, jmat_hwp, jmat_qwp ])
self.jmat_num = jmat_list.shape[0]
self.jmats = jmat_list
# 回転行列の反映
def __operate_rotate_mat(self):
self.theta_num = 17 # 回転角度の分割数
self.theta_list = -PI * np.arange(self.theta_num)/(self.theta_num-1)
# 回転行列
rotate_mat = np.array([
[np.cos(self.theta_list), -np.sin(self.theta_list)],
[np.sin(self.theta_list), np.cos(self.theta_list)],
])
rotate_mat = np.swapaxes(rotate_mat, 0,-1) # 次元の入れ替え -> 行列の転置
rotate_mat = rotate_mat[:,np.newaxis,np.newaxis,:,:]
# 逆回転行列
rev_rotate_mat = np.array([
[np.cos(-self.theta_list), -np.sin(-self.theta_list)],
[np.sin(-self.theta_list), np.cos(-self.theta_list)],
])
rev_rotate_mat = np.swapaxes(rev_rotate_mat, 0,-1) # 次元の入れ替え -> 行列の転置
rev_rotate_mat = rev_rotate_mat[:,np.newaxis,np.newaxis,:,:]
# 行列計算
jvecs_in = self.jvecs_in[:,:,np.newaxis,:,:]
jmats = self.jmats[np.newaxis,np.newaxis,:,:,:]
jvecs_out = np.matmul(jvecs_in, rev_rotate_mat) # 転置行列の内積計算
jvecs_out = np.matmul(jvecs_out, jmats) # 転置行列の内積計算
self.jvecs_out = np.matmul(jvecs_out, rotate_mat) # 転置行列の内積計算
#%% プロット値の計算
class CalcPlotValue:
def __init__(self):
z_in = np.linspace(0,2.5,26)
z_out = z_in+2.5
self.z_in = z_in * PI
self.z_out = z_out * PI
self.wave_in = np.exp(1.j*self.z_in)
self.wave_out = np.exp(1.j*self.z_out)
def get_wave_in(self, jvecs_in):
wave_in_x = jvecs_in[:,:,:,0,np.newaxis] * self.wave_in
wave_in_y = jvecs_in[:,:,:,1,np.newaxis] * self.wave_in
wave_in_x = np.real(wave_in_x)
wave_in_y = np.real(wave_in_y)
wave_in_x = self.drop_a_digit(wave_in_x)
wave_in_y = self.drop_a_digit(wave_in_y)
return [wave_in_x, wave_in_y]
def get_wave_out(self, jvecs_out):
wave_out_x = jvecs_out[:,:,:,:,0,np.newaxis] * self.wave_out
wave_out_y = jvecs_out[:,:,:,:,1,np.newaxis] * self.wave_out
wave_out_x = np.real(wave_out_x)
wave_out_y = np.real(wave_out_y)
wave_out_x = self.drop_a_digit(wave_out_x)
wave_out_y = self.drop_a_digit(wave_out_y)
return [wave_out_x, wave_out_y]
def drop_a_digit(self, x):
return np.round(x, DROP_DECIMALS)
def make_mesh(self, x):
elem0 = ((x)==0)
elenum0 = np.where(elem0)[0]
u0 = elenum0[np.cumsum(elem0)-1]
u = (np.delete(u0,elenum0))
v0 = np.arange(len(u0))
v = (np.delete(v0,(elenum0)))
w = v+1
return u,v,w
def make_mesh_line(self, x,z):
dz = z[1]-z[0]
signs = np.sign(x)
indices = np.where(signs[:-1]!=signs[1:])[0]
x_0lower = np.abs(np.real(x[indices]))
x_0upper = np.abs(np.real(x[indices+1]))
z_0position = z[indices]+x_0lower/(x_0lower+x_0upper)*dz
x = np.insert(x,indices+1,0)
z = np.insert(z,indices+1,z_0position)
x = np.hstack((0,x,0))
z = np.hstack((z[0],z,z[-1]))
z = self.drop_a_digit(z)
u,v,w = self.make_mesh(np.real(x))
return x,z,u,v,w
def make_opt_elems(self, theta_list):
x = [1.13*np.cos(PI/4 + theta_list), 1.13*np.cos(PI*3/4 + theta_list),
1.13*np.cos(PI*5/4 + theta_list), 1.13*np.cos(PI*7/4 + theta_list) ]
y = [1.13*np.sin(PI/4 + theta_list), 1.13*np.sin(PI*3/4 + theta_list),
1.13*np.sin(PI*5/4 + theta_list), 1.13*np.sin(PI*7/4 + theta_list) ]
z = [2.5*PI]*4
x = self.drop_a_digit(x)
y = self.drop_a_digit(y)
z = self.drop_a_digit(z)
return x,y,z
def make_opt_elem_axis(self, theta_list):
x = [-.8*np.cos(theta_list),.8*np.cos(theta_list)]
y = [-.8*np.sin(theta_list),.8*np.sin(theta_list)]
z = [2.5*PI]*2
x = self.drop_a_digit(x)
y = self.drop_a_digit(y)
z = self.drop_a_digit(z)
return x,y,z
#%% プロットトレースの作成
class MakeTrace:
def __init__(self, type):
self.type = type
if self.type == "mesh3d":
self.make_mesh3d_obj()
elif self.type == "scatter3d":
self.make_scatter3d_obj()
elif self.type == "cone":
self.make_cone_obj()
else:
pass
def make_mesh3d_obj(self):
plot_trace = dict(
x = [], y = [], z = [],
i = [], j = [], k = [],
#type":"mesh3d",
color = None,
opacity = 0.,
scene = "scene1",
visible = False,
text = "",
hoverinfo = "text",
)
self.plot_obj = go.Mesh3d(plot_trace)
def make_scatter3d_obj(self):
plot_trace = dict(
x = [], y = [], z = [],
#"type":"scatter3d",
mode = "lines",
line = dict(color = None, width = 1),
opacity = 0.,
scene = "scene1",
visible = False,
text = "",
hoverinfo = "text",
)
self.plot_obj = go.Scatter3d(plot_trace)
def make_cone_obj(self):
plot_trace = dict(
x = [], y = [], z = [],
u = [], v = [], w = [],
showscale = False,
colorscale = None,
scene = "scene1",
visible = False,
hoverinfo = "none",
)
self.plot_obj = go.Cone(plot_trace)
def add_to_fig(self, plotly_fig):
plotly_fig.add_trace(self.plot_obj)
#%%
if __name__ == '__main__':
fig = go.Figure()
#%% ジョーンズベクトル計算
calc_jvecs = CalcJVecs()
#[theta, jvec, jmat, :,:]
jvecs_in = calc_jvecs.jvecs_in # 入射側ジョーンズベクトル
jvecs_out = calc_jvecs.jvecs_out # 出射側ジョーンズベクトル
jvec_num = calc_jvecs.jvec_num # 出射側ジョーンズベクトル(偏波)種の数
jmat_num = calc_jvecs.jmat_num # ジョーンズマトリックス(光学素子)の数
theta_num = calc_jvecs.theta_num # 角度
#%% プロット値計算
calc_plot_value = CalcPlotValue()
wave_in_x, wave_in_y = calc_plot_value.get_wave_in(jvecs_in) # 入射光のプロット波形
wave_out_x, wave_out_y = calc_plot_value.get_wave_out(jvecs_out) # 出射光のプロット波形
z_in = calc_plot_value.z_in
z_out = calc_plot_value.z_out
#%%
x_opt_elem, y_opt_elem, z_opt_elem = calc_plot_value.make_opt_elems(calc_jvecs.theta_list) # 光学素子
x_elem_axis, y_elem_axis, z_elem_axis = calc_plot_value.make_opt_elem_axis(calc_jvecs.theta_list) # 光学素子の軸
#%% プロットトレースの設定
# trace1
trace_in_mesh_x = MakeTrace("mesh3d")
trace_in_mesh_x.plot_obj.update(color = "#00f")
trace_in_mesh_x.plot_obj.update(text = "electric field of incident light
in y direction, EY")
# trace2
trace_in_mesh_y = MakeTrace("mesh3d")
trace_in_mesh_y.plot_obj.update(color = "#f00")
trace_in_mesh_y.plot_obj.update(text = "electric field of incident light
in x direction, EX")
# trace3
trace_in_line = MakeTrace("scatter3d")
trace_in_line.plot_obj.update(line_color = "#1f0000")
trace_in_line.plot_obj.update(text = "electric field of incident light, E")
# trace4
trace_start_line = MakeTrace("scatter3d")
trace_start_line.plot_obj.update(line_color = "#1f0000", line_width = 4)
trace_start_line.plot_obj.update(text = "electric field of incident light,
E, at x-y plane")
# trace5
trace_out_mesh_x = MakeTrace("mesh3d")
trace_out_mesh_x.plot_obj.update(color = "#009999")
trace_out_mesh_x.plot_obj.update(text = "electric field of transmitted light
in y direction, EY")
# trace6
trace_out_mesh_y = MakeTrace("mesh3d")
trace_out_mesh_y.plot_obj.update(color = "#990099")
trace_out_mesh_y.plot_obj.update(text = "electric field of transmitted light
in x direction, EX")
# trace7
trace_out_line = MakeTrace("scatter3d")
trace_out_line.plot_obj.update(line_color = "#1f0000")
trace_out_line.plot_obj.update(text = "electric field of transmitted light, E")
# trace8
trace_end_line = MakeTrace("scatter3d")
trace_end_line.plot_obj.update(line_color = "#1f0000", line_width = 4)
trace_end_line.plot_obj.update(text = "electric field of transmitted light,
E, at x-y plane")
# else
trace_opt_elem = MakeTrace("mesh3d")
trace_opt_elem.plot_obj.update(color = "#000", opacity = 0.2, visible = True)
trace_opt_elem.plot_obj.update(text = "optical element")
trace_elem_axis = MakeTrace("scatter3d")
trace_elem_axis.plot_obj.update(line_color = "#fff", line_width = 4, opacity = 1, visible = True)
trace_elem_axis.plot_obj.update(text = "polarization axis of polarizer
(or fast axis of half-wave plate
and quarter-wave plate)")
trace_cone = MakeTrace("cone")
trace_cone.plot_obj.update(colorscale = "Blues", visible = True)
#%% トレースのプロット
for j in range(jvec_num):
x_in = wave_in_x[0,j,0,:]
y_in = wave_in_y[0,j,0,:]
x_in_mesh, z_in_mesh_x, u_in_x, v_in_x, w_in_x = calc_plot_value.make_mesh_line(x_in,z_in)
y_in_mesh, z_in_mesh_y, u_in_y, v_in_y, w_in_y = calc_plot_value.make_mesh_line(y_in,z_in)
for k in range(jmat_num):
x_out = wave_out_x[0,j,k,0,:]
y_out = wave_out_y[0,j,k,0,:]
x_out_mesh, z_out_mesh_x, u_out_x, v_out_x, w_out_x = calc_plot_value.make_mesh_line(x_out,z_out)
y_out_mesh, z_out_mesh_y, u_out_y, v_out_y, w_out_y = calc_plot_value.make_mesh_line(y_out,z_out)
# trace1
trace_in_mesh_x.plot_obj.update(
x = 0*z_in_mesh_y, y = y_in_mesh, z = z_in_mesh_y,
i = u_in_y, j = v_in_y, k = w_in_y,
)
trace_in_mesh_x.add_to_fig(fig)
# trace2
trace_in_mesh_y.plot_obj.update(
x = x_in_mesh, y = 0*z_in_mesh_x, z = z_in_mesh_x,
i = u_in_x, j = v_in_x, k = w_in_x,
)
trace_in_mesh_y.add_to_fig(fig)
# trace3
trace_in_line.plot_obj.update(
x = x_in, y = y_in, z = z_in,
)
trace_in_line.add_to_fig(fig)
# trace4
trace_start_line.plot_obj.update(
x = x_in, y = y_in, z = 0*z_in,
)
trace_start_line.add_to_fig(fig)
# trace5
trace_out_mesh_x.plot_obj.update(
x = 0*z_out_mesh_y, y = y_out_mesh, z = z_out_mesh_y,
i = u_out_y, j = v_out_y, k = w_out_y,
)
trace_out_mesh_x.add_to_fig(fig)
# trace6
trace_out_mesh_y.plot_obj.update(
x = x_out_mesh, y = 0*z_out_mesh_x, z = z_out_mesh_x,
i = u_out_x, j = v_out_x, k = w_out_x,
)
trace_out_mesh_y.add_to_fig(fig)
# trace7
trace_out_line.plot_obj.update(
x = x_out, y = y_out, z = z_out,
)
trace_out_line.add_to_fig(fig)
# trace8
trace_end_line.plot_obj.update(
x = x_out, y = y_out, z = [z_out[-1]]*len(z_out),
)
trace_end_line.add_to_fig(fig)
# optical element
#%%
trace_opt_elem.plot_obj.update(
x = x_opt_elem[:,0], y = y_opt_elem[:,0], z = z_opt_elem[:],
i=[0,0], j=[1,2], k=[2,3],
)
trace_opt_elem.add_to_fig(fig)
# axis of optical element
trace_elem_axis.plot_obj.update(
x = x_elem_axis[:,0], y = y_elem_axis[:,0], z = z_elem_axis[:]
)
trace_elem_axis.add_to_fig(fig)
# arrow
trace_cone.plot_obj.update(
x=[0], y=[0], z=[5*PI],
u=[0], v=[0], w=[2],
)
trace_cone.add_to_fig(fig)
#%% 初期表示設定
fig_num = 8
for k in range(jmat_num):
for i in range(fig_num):
fig.data[fig_num*k*jmat_num+i]["visible"] = True
opacities=[0.4, 0.4, 1, 1, 0.4, 0.4, 1, 1]
for j in range(jvec_num):
for i in range(fig_num):
fig.data[fig_num*j+i]["opacity"] = opacities[i]
#%% 変数切り替え設定1
steps1=[]
for i in range(theta_num):
theta = calc_jvecs.theta_list[i]
step1=dict(
method="restyle",
label='%dπ/%d' %(4-i,theta_num-1),
args=[dict(x = [], y = [], z = [], i = [], j = [], k = [],)]
)
for j in range(jvec_num):
x_in = wave_in_x[0,j,0,:]
y_in = wave_in_y[0,j,0,:]
x_in_mesh, z_in_mesh_x, u_in_x, v_in_x, w_in_x = calc_plot_value.make_mesh_line(x_in,z_in)
y_in_mesh, z_in_mesh_y, u_in_y, v_in_y, w_in_y = calc_plot_value.make_mesh_line(y_in,z_in)
for k in range(jmat_num):
x_out = wave_out_x[i,j,k,0,:]
y_out = wave_out_y[i,j,k,0,:]
x_out_mesh, z_out_mesh_x, u_out_x, v_out_x, w_out_x = calc_plot_value.make_mesh_line(x_out,z_out)
y_out_mesh, z_out_mesh_y, u_out_y, v_out_y, w_out_y = calc_plot_value.make_mesh_line(y_out,z_out)
step1["args"][0]["x"].extend([
0*z_in_mesh_y, x_in_mesh, x_in, x_in,
0*z_out_mesh_y, x_out_mesh, x_out, x_out
])
step1["args"][0]["y"].extend([
y_in_mesh, 0*z_in_mesh_x, y_in, y_in,
y_out_mesh, 0*z_out_mesh_x, y_out, y_out
])
step1["args"][0]["z"].extend([
z_in_mesh_y, z_in_mesh_x, z_in, 0*z_in,
z_out_mesh_y, z_out_mesh_x, z_out, [z_out[-1]]*len(z_out)
])
step1["args"][0]["i"].extend([u_in_y, u_in_x, None, None, u_out_y, u_out_x, None, None])
step1["args"][0]["j"].extend([v_in_y, v_in_x, None, None, v_out_y, v_out_x, None, None])
step1["args"][0]["k"].extend([w_in_y, w_in_x, None, None, w_out_y, w_out_x, None, None])
step1["args"][0]["x"].extend([
x_opt_elem[:,i], x_elem_axis[:,i], [0]
])
step1["args"][0]["y"].extend([
y_opt_elem[:,i], y_elem_axis[:,i], [0]
])
step1["args"][0]["z"].extend([
z_opt_elem[:], z_elem_axis[:], [5*PI]])
step1["args"][0]["i"].extend([[0,0],None,[0]])
step1["args"][0]["j"].extend([[1,2],None,[0]])
step1["args"][0]["k"].extend([[2,3],None,[2]])
steps1.append(step1)
#%% 変数切り替え設定2
steps2=[]
labels2=["polarizer", "half-wave (λ/2) plate", "quarter-wave(λ/4) plate"]
for j in range(jvec_num):
step2=dict(
method="restyle",
label=labels2[j],
args=["visible", [False] * len(fig.data)],
)
for k in range(jmat_num):
for i in range(fig_num):
step2["args"][1][fig_num*(j+k*jvec_num)+i] = True
step2["args"][1][len(fig.data)-3] = True
step2["args"][1][len(fig.data)-2] = True
step2["args"][1][len(fig.data)-1] = True
steps2.append(step2)
#%% 変数切り替え設定3
steps3=[]
labels3=["linear polarization", "elliptic polarization", "circular polarization"]
for k in range(jmat_num):
step3=dict(
method="restyle",
label=labels3[k],
args=["opacity", [0] * len(fig.data)],
)
for j in range(jvec_num):
for i in range(fig_num):
step3["args"][1][fig_num*(jmat_num*k+j)+i] = opacities[i]
step3["args"][1][len(fig.data)-3] = 0.2
step3["args"][1][len(fig.data)-2] = 1
step3["args"][1][len(fig.data)-1] = 1
steps3.append(step3)
#%% レイアウト設定
sliders = [dict(
active = 0,
currentvalue = dict(prefix = "θ="),
pad = dict(t = 50, r = 20, l = 10),
steps = steps1
)]
updatemenus = list([
dict(active = 0,
direction = "up",
x = 0.18,
y = -0.1,
xanchor = 'left',
yanchor = 'bottom',
buttons = steps3),
dict(active = 0,
direction = "up",
x = 0.68,
y = -0.1,
xanchor = 'left',
yanchor = 'bottom',
buttons = steps2
)
])
camera = dict(
up = dict(x = 0, y = 0.5, z = 0),
center = dict(x = 0.1, y = -0.2, z = 0),
eye = dict(x = -0.9, y = 0.3, z = -1.2),
)
fig['layout'].update(
scene_camera = camera,
autosize = True,
margin = dict(l = 0.0, r = 0.0, b = 130, t = 0),
showlegend = False,
sliders = sliders,
paper_bgcolor = '#414141',
plot_bgcolor = '#ffe3e3',
font = dict(color = "#fff"),
updatemenus = updatemenus,
height = 500, width = 600,
annotations = [
dict(text = "incident light:", x = 0.02, xref = "paper",
y = -0.08, yref = "paper", align = "left", showarrow = False),
dict(text = "optical element:", x = 0.58, xref = "paper",
y = -0.08, yref = "paper", showarrow = False),
])
fig['layout']['scene1'].update(aspectratio = dict(x = 0.7,y = 0.7,z = 1.5),
xaxis = dict(color = "#fff", linecolor = "#fff", gridcolor = "#eee", range = [-1.6,1.6], showticklabels = False),
yaxis = dict(color = "#fff", linecolor = "#fff", gridcolor = "#eee", range = [-1.6,1.6], showticklabels = False),
zaxis = dict(color = "#fff", linecolor = "#fff", gridcolor = "#eee", showticklabels = False))
#%% グラフの描写
py.iplot(fig)
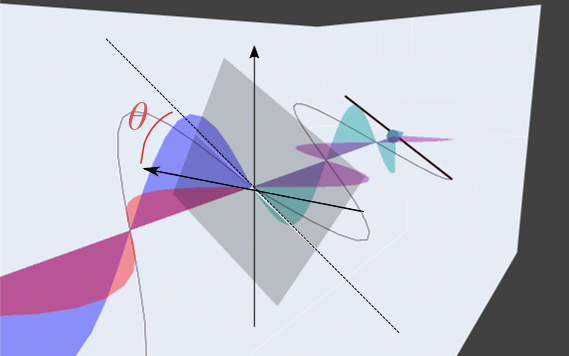
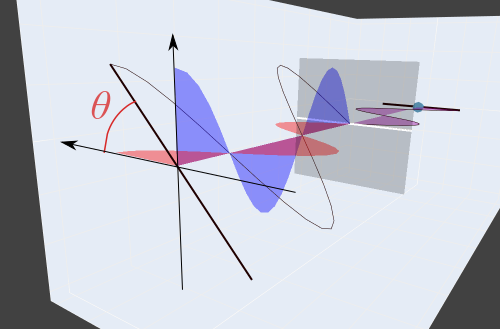
プロット2 :入射光の回転
プロットしているもの、操作方法は上のプロット1と基本的に変わりません。ただしスライダーを動かしたときに回転するのは、光学素子(偏光板, 波長板)ではなく入射光となっています。
ソースコード
【表示する】
#!/usr/bin/env python
# -*- coding: utf-8 -*-
#%% モジュールのインポート
import plotly.graph_objects as go
import plotly.offline as py
import numpy as np
py.init_notebook_mode(connected = True)
#%% パラメータ設定
PI = np.pi
THETA_OPT_ELEM = 0 # 光学素子の角度
DROP_DECIMALS = 3 # 出力値の桁数
#%% ジョーンズマトリックス計算
class CalcJVecs:
def __init__(self):
self.__make_jmat_list()
self.__make_in_jvec_list()
self.__operate_rotate_mat()
self.__make_output_jvec_list()
# 入射光のジョーンズベクトル
def __make_in_jvec_list(self):
jvec_liner = [1,1] / np.sqrt(2) # 直線偏波
jvec_ellipt= [np.exp(1.j*PI/5),1] / np.sqrt(2) # 楕円偏波
jvec_circul= [1.j,1] / np.sqrt(2) # 円偏波
jvec_in_list = np.array([jvec_liner, jvec_ellipt, jvec_circul])
self.jvec_in_list = jvec_in_list
self.jvec_num = self.jvec_in_list.shape[0]
# 光学素子のジョーンズマトリックス
def __make_jmat_list(self):
jmat_pol = [[1,0],[0,0]] # 偏光板
jmat_hwp = [[1,0],[0,-1]] # ラムダ/2 波長板
jmat_qwp = [[1,0],[0,1.j]] # ラムダ/4 波長板
jmat_list = np.array([jmat_pol, jmat_hwp, jmat_qwp ])
self.jmat_num = jmat_list.shape[0]
self.jmats = jmat_list
# 回転行列の反映
def __operate_rotate_mat(self):
self.theta_num = 17 # 回転角度の分割数
self.theta_list = -PI * np.arange(self.theta_num)/(self.theta_num-1)
rotate_mat = np.array([ # 回転行列
[np.cos(self.theta_list), -np.sin(self.theta_list)],
[np.sin(self.theta_list), np.cos(self.theta_list)],
])
rotate_mat = np.swapaxes(rotate_mat, 0,-1) # 次元の入れ替え -> 行列の転置
rotate_mat = rotate_mat[:,np.newaxis,:,:]
jvec_in_list = self.jvec_in_list[np.newaxis,:,np.newaxis,:]
self.jvecs_in = np.matmul(jvec_in_list,rotate_mat) # 転置行列の内積計算
# 出射光のジョーンズベクトル
def __make_output_jvec_list(self):
jvecs_in = self.jvecs_in[:,:,np.newaxis,:,:]
jmats = self.jmats[np.newaxis,np.newaxis,:,:,:]
self.jvecs_out = np.matmul(jvecs_in, jmats) # 転置行列の内積計算
#%% プロット値の計算
class CalcPlotValue:
def __init__(self):
z_in = np.linspace(0,2.5,26)
z_out = z_in+2.5
self.z_in = z_in * PI
self.z_out = z_out * PI
self.wave_in = np.exp(1.j*self.z_in)
self.wave_out = np.exp(1.j*self.z_out)
def get_wave_in(self, jvecs_in):
wave_in_x = jvecs_in[:,:,:,0,np.newaxis] * self.wave_in
wave_in_y = jvecs_in[:,:,:,1,np.newaxis] * self.wave_in
wave_in_x = np.real(wave_in_x)
wave_in_y = np.real(wave_in_y)
wave_in_x = self.drop_a_digit(wave_in_x)
wave_in_y = self.drop_a_digit(wave_in_y)
return [wave_in_x, wave_in_y]
def get_wave_out(self, jvecs_out):
wave_out_x = jvecs_out[:,:,:,:,0,np.newaxis] * self.wave_out
wave_out_y = jvecs_out[:,:,:,:,1,np.newaxis] * self.wave_out
wave_out_x = np.real(wave_out_x)
wave_out_y = np.real(wave_out_y)
wave_out_x = self.drop_a_digit(wave_out_x)
wave_out_y = self.drop_a_digit(wave_out_y)
return [wave_out_x, wave_out_y]
def drop_a_digit(self, x):
return np.round(x, DROP_DECIMALS)
def make_mesh(self, x):
elem0 = ((x)==0)
elenum0 = np.where(elem0)[0]
u0 = elenum0[np.cumsum(elem0)-1]
u = (np.delete(u0,elenum0))
v0 = np.arange(len(u0))
v = (np.delete(v0,(elenum0)))
w = v+1
return u,v,w
def make_mesh_line(self, x,z):
dz = z[1]-z[0]
signs = np.sign(x)
indices = np.where(signs[:-1]!=signs[1:])[0]
x_0lower = np.abs(np.real(x[indices]))
x_0upper = np.abs(np.real(x[indices+1]))
z_0position = z[indices]+x_0lower/(x_0lower+x_0upper)*dz
x = np.insert(x,indices+1,0)
z = np.insert(z,indices+1,z_0position)
x = np.hstack((0,x,0))
z = np.hstack((z[0],z,z[-1]))
z = self.drop_a_digit(z)
u,v,w = self.make_mesh(np.real(x))
return x,z,u,v,w
#%% プロットトレースの作成
class MakeTrace:
def __init__(self, type):
self.type = type
if self.type == "mesh3d":
self.make_mesh3d_obj()
elif self.type == "scatter3d":
self.make_scatter3d_obj()
elif self.type == "cone":
self.make_cone_obj()
else:
pass
def make_mesh3d_obj(self):
plot_trace = dict(
x = [], y = [], z = [],
i = [], j = [], k = [],
#type":"mesh3d",
color = None,
opacity = 0.,
scene = "scene1",
visible = False,
text = "",
hoverinfo = "text",
)
self.plot_obj = go.Mesh3d(plot_trace)
def make_scatter3d_obj(self):
plot_trace = dict(
x = [], y = [], z = [],
#"type":"scatter3d",
mode = "lines",
line = dict(color = None, width = 1),
opacity = 0.,
scene = "scene1",
visible = False,
text = "",
hoverinfo = "text",
)
self.plot_obj = go.Scatter3d(plot_trace)
def make_cone_obj(self):
plot_trace = dict(
x = [], y = [], z = [],
u = [], v = [], w = [],
showscale = False,
colorscale = None,
scene = "scene1",
visible = False,
hoverinfo = "none",
)
self.plot_obj = go.Cone(plot_trace)
def add_to_fig(self, plotly_fig):
plotly_fig.add_trace(self.plot_obj)
#%%
if __name__ == '__main__':
fig = go.Figure()
#%% ジョーンズベクトル計算
calc_jvecs = CalcJVecs()
#[theta, jvec, jmat, :,:]
jvecs_in = calc_jvecs.jvecs_in # 入射側ジョーンズベクトル
jvecs_out = calc_jvecs.jvecs_out # 出射側ジョーンズベクトル
jvec_num = calc_jvecs.jvec_num # 出射側ジョーンズベクトル(偏波)種の数
jmat_num = calc_jvecs.jmat_num # ジョーンズマトリックス(光学素子)の数
theta_num = calc_jvecs.theta_num # 角度
#%% プロット値計算
calc_plot_value = CalcPlotValue()
wave_in_x, wave_in_y = calc_plot_value.get_wave_in(jvecs_in) # 入射光のプロット波形
wave_out_x, wave_out_y = calc_plot_value.get_wave_out(jvecs_out) # 出射光のプロット波形
z_in = calc_plot_value.z_in
z_out = calc_plot_value.z_out
#%% プロットトレースの設定
# trace1
trace_in_mesh_x = MakeTrace("mesh3d")
trace_in_mesh_x.plot_obj.update(color = "#00f")
trace_in_mesh_x.plot_obj.update(text = "electric field of incident light
in y direction, EY")
# trace2
trace_in_mesh_y = MakeTrace("mesh3d")
trace_in_mesh_y.plot_obj.update(color = "#f00")
trace_in_mesh_y.plot_obj.update(text = "electric field of incident light
in x direction, EX")
# trace3
trace_in_line = MakeTrace("scatter3d")
trace_in_line.plot_obj.update(line_color = "#1f0000")
trace_in_line.plot_obj.update(text = "electric field of incident light, E")
# trace4
trace_start_line = MakeTrace("scatter3d")
trace_start_line.plot_obj.update(line_color = "#1f0000", line_width = 4)
trace_start_line.plot_obj.update(text = "electric field of incident light,
E, at x-y plane")
# trace5
trace_out_mesh_x = MakeTrace("mesh3d")
trace_out_mesh_x.plot_obj.update(color = "#009999")
trace_out_mesh_x.plot_obj.update(text = "electric field of transmitted light
in y direction, EY")
# trace6
trace_out_mesh_y = MakeTrace("mesh3d")
trace_out_mesh_y.plot_obj.update(color = "#990099")
trace_out_mesh_y.plot_obj.update(text = "electric field of transmitted light
in x direction, EX")
# trace7
trace_out_line = MakeTrace("scatter3d")
trace_out_line.plot_obj.update(line_color = "#1f0000")
trace_out_line.plot_obj.update(text = "electric field of transmitted light, E")
# trace8
trace_end_line = MakeTrace("scatter3d")
trace_end_line.plot_obj.update(line_color = "#1f0000", line_width = 4)
trace_end_line.plot_obj.update(text = "electric field of transmitted light,
E, at x-y plane")
# else
trace_opt_elem = MakeTrace("mesh3d")
trace_opt_elem.plot_obj.update(color = "#000", opacity = 0.2, visible = True)
trace_opt_elem.plot_obj.update(text = "optical element")
trace_elem_axis = MakeTrace("scatter3d")
trace_elem_axis.plot_obj.update(line_color = "#fff", line_width = 4, opacity = 1, visible = True)
trace_elem_axis.plot_obj.update(text = "polarization axis of polarizer
(or fast axis of half-wave plate
and quarter-wave plate)")
trace_cone = MakeTrace("cone")
trace_cone.plot_obj.update(colorscale = "Blues", visible = True)
#%% トレースのプロット
for j in range(jvec_num):
x_in = wave_in_x[0,j,0,:]
y_in = wave_in_y[0,j,0,:]
x_in_mesh, z_in_mesh_x, u_in_x, v_in_x, w_in_x = calc_plot_value.make_mesh_line(x_in,z_in)
y_in_mesh, z_in_mesh_y, u_in_y, v_in_y, w_in_y = calc_plot_value.make_mesh_line(y_in,z_in)
for k in range(jmat_num):
x_out = wave_out_x[0,j,k,0,:]
y_out = wave_out_y[0,j,k,0,:]
x_out_mesh, z_out_mesh_x, u_out_x, v_out_x, w_out_x = calc_plot_value.make_mesh_line(x_out,z_out)
y_out_mesh, z_out_mesh_y, u_out_y, v_out_y, w_out_y = calc_plot_value.make_mesh_line(y_out,z_out)
# trace1
trace_in_mesh_x.plot_obj.update(
x = 0*z_in_mesh_y, y = y_in_mesh, z = z_in_mesh_y,
i = u_in_y, j = v_in_y, k = w_in_y,
)
trace_in_mesh_x.add_to_fig(fig)
# trace2
trace_in_mesh_y.plot_obj.update(
x = x_in_mesh, y = 0*z_in_mesh_x, z = z_in_mesh_x,
i = u_in_x, j = v_in_x, k = w_in_x,
)
trace_in_mesh_y.add_to_fig(fig)
# trace3
trace_in_line.plot_obj.update(
x = x_in, y = y_in, z = z_in,
)
trace_in_line.add_to_fig(fig)
# trace4
trace_start_line.plot_obj.update(
x = x_in, y = y_in, z = 0*z_in,
)
trace_start_line.add_to_fig(fig)
# trace5
trace_out_mesh_x.plot_obj.update(
x = 0*z_out_mesh_y, y = y_out_mesh, z = z_out_mesh_y,
i = u_out_y, j = v_out_y, k = w_out_y,
)
trace_out_mesh_x.add_to_fig(fig)
# trace6
trace_out_mesh_y.plot_obj.update(
x = x_out_mesh, y = 0*z_out_mesh_x, z = z_out_mesh_x,
i = u_out_x, j = v_out_x, k = w_out_x,
)
trace_out_mesh_y.add_to_fig(fig)
# trace7
trace_out_line.plot_obj.update(
x = x_out, y = y_out, z = z_out,
)
trace_out_line.add_to_fig(fig)
# trace8
trace_end_line.plot_obj.update(
x = x_out, y = y_out, z = [z_out[-1]]*len(z_out),
)
trace_end_line.add_to_fig(fig)
# optical element
x_opt_elem = np.round([1.13*np.cos(PI/4 + THETA_OPT_ELEM), 1.13*np.cos(PI*3/4 + THETA_OPT_ELEM),
1.13*np.cos(PI*5/4 + THETA_OPT_ELEM), 1.13*np.cos(PI*7/4 + THETA_OPT_ELEM) ], DROP_DECIMALS)
y_opt_elem = np.round([1.13*np.sin(PI/4 + THETA_OPT_ELEM), 1.13*np.sin(PI*3/4 + THETA_OPT_ELEM),
1.13*np.sin(PI*5/4 + THETA_OPT_ELEM), 1.13*np.sin(PI*7/4 + THETA_OPT_ELEM) ], DROP_DECIMALS)
z_opt_elem = np.round([2.5*PI]*4, DROP_DECIMALS)
trace_opt_elem.plot_obj.update(
x = x_opt_elem, y = y_opt_elem, z = z_opt_elem,
i=[0,0], j=[1,2], k=[2,3],
)
trace_opt_elem.add_to_fig(fig)
# axis of optical element
x_elem_axis = np.round([-.8*np.cos(THETA_OPT_ELEM),.8*np.cos(THETA_OPT_ELEM)], DROP_DECIMALS)
y_elem_axis = np.round([-.8*np.sin(THETA_OPT_ELEM),.8*np.sin(THETA_OPT_ELEM)], DROP_DECIMALS)
z_elem_axis = np.round([2.5*PI]*2, DROP_DECIMALS)
trace_elem_axis.plot_obj.update(
x = x_elem_axis, y = y_elem_axis, z = z_elem_axis,
)
trace_elem_axis.add_to_fig(fig)
# arrow
trace_cone.plot_obj.update(
x=[0], y=[0], z=[5*PI],
u=[0], v=[0], w=[2],
)
trace_cone.add_to_fig(fig)
#%% 初期表示設定
fig_num = 8
for k in range(jmat_num):
for i in range(fig_num):
fig.data[fig_num*k*jmat_num+i]["visible"] = True
opacities=[0.4, 0.4, 1, 1, 0.4, 0.4, 1, 1]
for j in range(jvec_num):
for i in range(fig_num):
fig.data[fig_num*j+i]["opacity"] = opacities[i]
#%% 変数切り替え設定1
steps1=[]
for i in range(theta_num):
theta = calc_jvecs.theta_list[i]
step1=dict(
method="restyle",
label='%dπ/%d' %(4-i,theta_num-1),
args=[dict(x = [], y = [], z = [], i = [], j = [], k = [],)]
)
for j in range(jvec_num):
x_in = wave_in_x[i,j,0,:]
y_in = wave_in_y[i,j,0,:]
x_in_mesh, z_in_mesh_x, u_in_x, v_in_x, w_in_x = calc_plot_value.make_mesh_line(x_in,z_in)
y_in_mesh, z_in_mesh_y, u_in_y, v_in_y, w_in_y = calc_plot_value.make_mesh_line(y_in,z_in)
for k in range(jmat_num):
x_out = wave_out_x[i,j,k,0,:]
y_out = wave_out_y[i,j,k,0,:]
x_out_mesh, z_out_mesh_x, u_out_x, v_out_x, w_out_x = calc_plot_value.make_mesh_line(x_out,z_out)
y_out_mesh, z_out_mesh_y, u_out_y, v_out_y, w_out_y = calc_plot_value.make_mesh_line(y_out,z_out)
step1["args"][0]["x"].extend([
0*z_in_mesh_y, x_in_mesh, x_in, x_in,
0*z_out_mesh_y, x_out_mesh, x_out, x_out
])
step1["args"][0]["y"].extend([
y_in_mesh, 0*z_in_mesh_x, y_in, y_in,
y_out_mesh, 0*z_out_mesh_x, y_out, y_out
])
step1["args"][0]["z"].extend([
z_in_mesh_y, z_in_mesh_x, z_in, 0*z_in,
z_out_mesh_y, z_out_mesh_x, z_out, [z_out[-1]]*len(z_out)
])
step1["args"][0]["i"].extend([u_in_y, u_in_x, None, None, u_out_y, u_out_x, None, None])
step1["args"][0]["j"].extend([v_in_y, v_in_x, None, None, v_out_y, v_out_x, None, None])
step1["args"][0]["k"].extend([w_in_y, w_in_x, None, None, w_out_y, w_out_x, None, None])
step1["args"][0]["x"].extend([
x_opt_elem, x_elem_axis, [0]
])
step1["args"][0]["y"].extend([
y_opt_elem, y_elem_axis, [0]
])
step1["args"][0]["z"].extend([
z_opt_elem, z_elem_axis, [5*PI]])
step1["args"][0]["i"].extend([[0,0],None,[0]])
step1["args"][0]["j"].extend([[1,2],None,[0]])
step1["args"][0]["k"].extend([[2,3],None,[2]])
steps1.append(step1)
#%% 変数切り替え設定2
steps2=[]
labels2=["polarizer", "half-wave (λ/2) plate", "quarter-wave(λ/4) plate"]
for j in range(jvec_num):
step2=dict(
method="restyle",
label=labels2[j],
args=["visible", [False] * len(fig.data)],
)
for k in range(jmat_num):
for i in range(fig_num):
step2["args"][1][fig_num*(j+k*jvec_num)+i] = True
step2["args"][1][len(fig.data)-3] = True
step2["args"][1][len(fig.data)-2] = True
step2["args"][1][len(fig.data)-1] = True
steps2.append(step2)
#%% 変数切り替え設定3
steps3=[]
labels3=["linear polarization", "elliptic polarization", "circular polarization"]
for k in range(jmat_num):
step3=dict(
method="restyle",
label=labels3[k],
args=["opacity", [0] * len(fig.data)],
)
for j in range(jvec_num):
for i in range(fig_num):
step3["args"][1][fig_num*(jmat_num*k+j)+i] = opacities[i]
step3["args"][1][len(fig.data)-3] = 0.2
step3["args"][1][len(fig.data)-2] = 1
step3["args"][1][len(fig.data)-1] = 1
steps3.append(step3)
#%% レイアウト設定
sliders = [dict(
active = 0,
currentvalue = dict(prefix = "θ="),
pad = dict(t = 50, r = 20, l = 10),
steps = steps1
)]
updatemenus = list([
dict(active = 0,
direction = "up",
x = 0.18,
y = -0.1,
xanchor = 'left',
yanchor = 'bottom',
buttons = steps3),
dict(active = 0,
direction = "up",
x = 0.68,
y = -0.1,
xanchor = 'left',
yanchor = 'bottom',
buttons = steps2
)
])
camera = dict(
up = dict(x = 0, y = 0.5, z = 0),
center = dict(x = 0.1, y = -0.2, z = 0),
eye = dict(x = -0.9, y = 0.3, z = -1.2),
)
fig['layout'].update(
scene_camera = camera,
autosize = True,
margin = dict(l = 0.0, r = 0.0, b = 130, t = 0),
showlegend = False,
sliders = sliders,
paper_bgcolor = '#414141',
plot_bgcolor = '#ffe3e3',
font = dict(color = "#fff"),
updatemenus = updatemenus,
height = 500, width = 600,
annotations = [
dict(text = "incident light:", x = 0.02, xref = "paper",
y = -0.08, yref = "paper", align = "left", showarrow = False),
dict(text = "optical element:", x = 0.58, xref = "paper",
y = -0.08, yref = "paper", showarrow = False),
])
fig['layout']['scene1'].update(aspectratio = dict(x = 0.7,y = 0.7,z = 1.5),
xaxis = dict(color = "#fff", linecolor = "#fff", gridcolor = "#eee", range = [-1.6,1.6], showticklabels = False),
yaxis = dict(color = "#fff", linecolor = "#fff", gridcolor = "#eee", range = [-1.6,1.6], showticklabels = False),
zaxis = dict(color = "#fff", linecolor = "#fff", gridcolor = "#eee", showticklabels = False))
#%% グラフの描写
py.iplot(fig)
偏光板, 波長板を傾けるとどうなるか
偏光板 ~クロスニコルに更に偏光板を加えると明るくなるのは?
偏光板の働きはイメージしやすいと思います。偏光板は透過軸に沿った直線偏光を切り出します。偏光の傾きと偏光板の透過軸があっていない場合でも、90度ずれていない限りは透過光が漏れ出ます(余弦成分だけ)。このとき入射偏波の傾きと偏光板の透過軸が近いほど多くの透過光が得られます。
ところで、偏光板2枚を90度傾けて重ねると光が通らない、いわゆるクロスニコルの状態があります。この間に3枚目の偏光板を45度傾けて重ねると、2枚の状態よりも光が通るようになることをご存じでしょうか。
これを知った当初は一体どうなっているのかイメージできませんでした。偏光板を単純なフィルタとして考えると、フィルタの数が多ければ多いほど透過する量が減っていくと感じたためです。
しかし光が偏光板の透過軸に沿って切られていくことを考えていくと腑に落ちます。偏光板の透過軸と入射偏波の向きがずれていると、確かに透過光強度は減衰します。しかしそれだけではなく、偏光板を通過すると偏光の傾きが偏光板の透過軸に変換されます。直線偏光の角度をいきなり90度に変換すると強度がゼロになってしまいますが、一部光を通す45度に変換する操作を間に加えることによって、入射光が一部漏れ出るようになるということです。このように偏光板は入射光の透過軸に沿った成分を切り出すフィルタであり、透過光の偏光の軸は偏光板の軸に変わります。
2/λ波長板
2/λ波長板を回転させると、入射した直線偏光・楕円偏光の角度が回転します。なぜそうなるのかというと、2/λ波長板の持つ2つの軸(スロー軸とファスト軸)のうちスロー軸に入った成分のみが半波長(λ/2)分位相がずれるためです。半波長位相がずれるということは、スロー軸成分の波の山が谷になり、符号が反転するということになり、ファスト軸と偏光軸の成す角度の符号も反転します。
このとき2/λ波長板を透過する前後での傾きの変化、つまり入射偏波軸と透過偏波軸の成す角度は2θとなります(θ:ファスト軸と入射偏波軸の成す角度)。以上のように、2/λ波長板の軸と入射偏波の軸の成す角θを変えると、透過光の偏波の軸は2θ分回転するということになります。
4/λ波長板
λ/4波長板もファスト軸とそこから90°傾いたスロー軸を持っています。ファスト軸に入る波に対して、スロー軸に入る波は位相がλ/4(90°)遅れて透過します。この挙動によって、入射偏波に対する波長板の角度をうまく調整すると、直線偏光を楕円または円偏光に変換することや、逆に楕円・円偏光を直線偏光に変換することができます。
直線偏光を円偏光に変換するときを考えてみます。直線偏光はx方向とy方向の2つの偏波成分に分解したときに、2つの偏波の位相は一致(波のタイミングが山と山 or 山と谷)しているので、λ/4波長板に入れると2つの偏波の位相はλ/4分(90°)ずれます。ここで波長板または入射光を回転させて、うまくファスト軸とスロー軸に1:1に入る角度に調整することで、円偏光をつくることができます。比率が1:1から1:0の間となる角度のときは楕円偏光となります。
次に円偏光・楕円偏光を直線偏光にするときを考えてみます。円偏光はx, y方向の偏波に分解すると、位相はλ/4(90°)ずれています。
これは分解するx, yの角度を変えても同様です。
そのためλ/4波長板に通すと位相差がゼロになるため直線偏光になります。楕円偏光は分解するx, y方向の角度によって、2つの波の位相差が違います。そのため、分解後の2つの波の位相差かλ/4(90°)になるように波長板または入射光を回転させると、円偏光になります。ちょうど楕円がxまたはy軸方向に伸びた形になるように角度調整したときが、これに相当します。
偏光をプロットするための数学的演算
おおまかな流れ
上のグラフで偏光の挙動をプロットし可視化しましたが、ジョーンズ計算法によって偏光の挙動を計算しています。ジョーンズ計算法についてはこちらの記事で取り扱いました。入射光の偏光状態を表すジョーンズベクトルに、光学素子による偏光操作に対応したジョーンズ行列を作用させることで、光学素子を通った後の透過光の偏光状態を表すジョーンズベクトルが得られます。ジョーンズベクトルのx成分にe^{iz}を掛けた実部をプロットすると偏光のx成分の波、y成分にe^{iz}を掛けた実部をプロットすると偏光のy成分の波となります。
入射偏波 or 光学素子を回転させないとき
上グラフでは、入射光として3種類の中から選択できます。3種類というのは、x軸から45度傾いた直線偏光, 45度傾いた楕円偏光, 円偏光です。これらの偏波は以下のようなx成分の強度・位相情報を持つ複素数とy成分の強度・位相情報を持つ複素数の組み合わせ、すなわちジョーンズベクトルによって示されます。
- x軸から45度傾いた直線偏光:$\displaystyle \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1\\ 1 \end{array} \right)$
- x軸から45度傾いた楕円偏光:$\displaystyle \frac{1}{\sqrt{2}} \left( \begin{array}{c} e^{\frac{\pi}{5}i}\\ 1 \end{array} \right)$ (※上のグラフと楕円率が異なる場合は、値が異なります)
- 円偏光:$\displaystyle \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1\\ i \end{array} \right)$
これら入射光のジョーンズベクトルに、光学素子の作用をするジョーンズ行列を作用させると透過光のジョーンズベクトルが得られます。上グラフでのジョーンズ行列は以下の3つから選べるようになっています。
- 偏光板(透過軸x方向):$\displaystyle \left( \begin{array}{cc} 1&0\\ 0&0 \end{array} \right)$
- λ/2波長板(ファスト軸x方向):$\displaystyle \left( \begin{array}{cc} 1&0 \\ 0 & -1 \end{array} \right)$
- λ/4波長板(ファスト軸x方向):$\displaystyle \left( \begin{array}{cc} 1 & 0 \\ 0 & -i \end{array} \right)$
入射偏波 or 光学素子を回転させたとき
入射光を回転させて偏波が傾いたときは、入射光のジョーンズベクトルに回転行列を作用させることによってそのときの偏波を表現することができます。x軸方向に透過軸が向いた直線偏光のジョーンズベクトルは$\displaystyle \left( \begin{array}{c} 1 \\ 0 \end{array} \right)$
ですので、x軸からΘ度傾いた直線偏光は$\displaystyle \left( \begin{array}{c} 1 \\ 0 \end{array} \right)$と回転行列$\displaystyle \left( \begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array} \right)$の積、すなわち
$$\displaystyle \left( \begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array} \right)\left( \begin{array}{c} 1 \\ 0 \end{array} \right)=\left( \begin{array}{c} \cos \theta \\ \sin\theta \end{array} \right)$$
となります。
一方、入射光は回転させず、光学素子を回転させるときですが、上記の入射光を回転させたときを応用して考えます。入射光が回転したときも光学素子が回転したときも、いずれも入射偏波の軸と光学素子の軸(偏光板の透過軸や波長板のファスト軸)のなす角度は同じです。そのため光学素子の入射光への作用はいずれも等しく、光学素子によって作り出される透過光の偏波は同じと言えます。違う点は透過光の傾きだけです。
以上のことから、光学素子を傾けたときの考え方は、まず光学素子の傾きが0になるように光学素子を逆に傾け、入射光も一緒に傾けます。すると入射光が傾き、光学素子は固定された状態、すなわち上記と同じ入射光を回転さた状況になります。このときの透過光の偏波のジョーンズ行列は上記の通りに得られます。透過光の偏波が計算できたら、入射光・光学素子・透過光のすべてを一緒に初期の状態に傾けると、全体像として光学素子のみを傾けていることになります。つまり光学素子が傾いたときの計算は、まず入射光の偏波が傾いているとして計算しその後、入射偏波を傾けた分だけ系全体を回転させて元に戻すという手順を踏みます。
例として、x軸方向の直線偏光を入射光として、透過軸がΘ度傾いた偏光板に透過させたときの透過光のジョーンズベクトルを算出してみます。x軸方向の直線偏光のジョーンズベクトルは$\displaystyle \left( \begin{array}{c} 1 \\ 0 \end{array} \right)$です。まずは入射光と偏光板を同時に-Θ度傾けるので、入射光に-Θ度回転させるための回転行列を作用させます
$$\displaystyle \left( \begin{array}{cc} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta) & \cos(-\theta) \end{array} \right)\left( \begin{array}{c} 1 \\ 0 \end{array} \right)$$
。
このとき偏光板の透過軸の傾きは初期のΘ度から-Θ度傾けて0度となっている、つまりx軸方向に透過軸が向いているので、偏光板のジョーンズ行列は$\displaystyle \left( \begin{array}{cc} 1&0 \\ 0&0 \end{array} \right)$です。このジョーンズ行列を-Θ度傾けた入射光に作用させます
$$\displaystyle \left( \begin{array}{cc} 1 &0 \\0&0 \end{array} \right)\left( \begin{array}{cc} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta)&\cos(-\theta) \end{array} \right)\left( \begin{array}{c} 1 \\ 0 \end{array} \right)$$
これで偏光板を透過後のジョーンズ行列が得られますが、入射光と偏光板を-Θ度傾けたままなので、これをもとに戻します。つまりΘ度の回転行列を作用させます。
$$\displaystyle \left( \begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta&\cos\theta\end{array}\right)\left( \begin{array}{cc} 1 &0 \\0&0 \end{array} \right)\left( \begin{array}{cc} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta)&\cos(-\theta) \end{array} \right)\left( \begin{array}{c} 1 \\ 0 \end{array} \right)$$
以上で偏光板を回転(傾けた)ときの透過光のジョーンズベクトルが得られます。入射光のジョーンズベクトルに作用させる行列部分をまとめると、最終的には
$$\displaystyle \left( \begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta&\cos\theta\end{array}\right)\left( \begin{array}{cc} 1 &0 \\0&0 \end{array} \right)\left( \begin{array}{cc} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta)&\cos(-\theta) \end{array} \right)\left( \begin{array}{c} 1 \\ 0 \end{array} \right)=\left( \begin{array}{cc} \cos^2\theta & \cos\theta \sin\theta \\ \sin\theta\cos\theta & \sin^2\theta \end{array} \right)$$
の行列がΘ度傾いた偏光板のジョーンズ行列になります。傾いた波長板についても同様に考えてジョーンズ行列が得られます。
x軸からΘ度傾いた光学素子のジョーンズ行列をまとめると以下の通りになります。
- 偏光板:$\displaystyle \left( \begin{array}{cc} \cos^2\theta & \cos\theta \sin\theta \\ \sin\theta\cos\theta & \sin^2\theta \end{array} \right)$
- λ/2波長板:$\displaystyle \left( \begin{array}{cc} \cos(2\theta) & \sin(2\theta) \\ \sin(2\theta) & -\cos(2\theta) \end{array} \right)$
- λ/4波長板:$\displaystyle \left( \begin{array}{cc} 1+i\cos(2\theta) & i\sin(2\theta) \\ i\sin(2\theta) & 1-i\cos(2\theta) \end{array} \right)$
まとめ
偏光板、λ/2波長板およびλ/4波長板の光学素子(または入射偏波)を回転させたときの透過光の偏波がどうなるのか取り扱ってみました。偏光板では切り出す直線偏光の角度と強度、λ/2波長板では偏光の角度、λ/4波長板では偏光の形を変えることができます。