【動くグラフ】物理的な波の扱いのパラメータと複素数表示
投稿日:2021年7月18日 更新日:
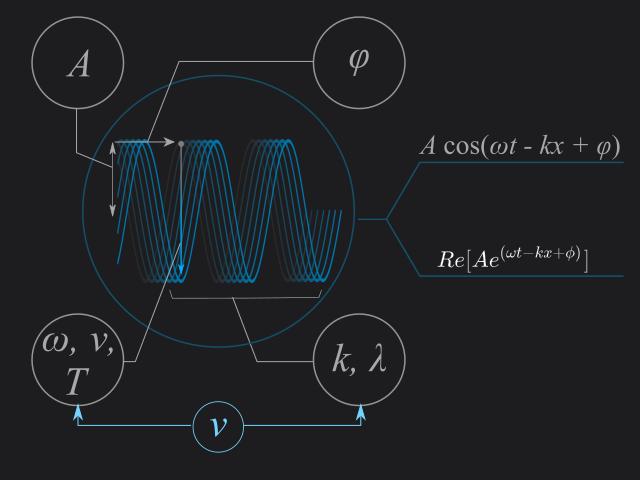
工学系のエンジニアや研究者には波を扱うことがよくあり、信号解析や設計等を行う上で数学的な扱いは必須となります。理系大学出身の人は、振動・波動の講義で触れたことがあるのではないでしょうか。ここでは波を表す周期関数であるサイン波(正弦波)・コサイン波(余弦波)の基礎的なパラメーターのことをまとめ、複素数表示の形式についても触れておきます。
波を決定する4つのパラメーター
波として、数学で以下のような三角関数を習うと思います。
- サイン波: $\sin(\theta)$
- コサイン波: $\cos(\theta)$
これらの関数を使って、物理的な波は以下のように示されることが多いです。
$$ A \cos(\omega t-kx+\phi) $$
- $A$:振幅・・・波の大きさ
- $\omega$:角周波数・・・時間経過による波の振動の多さ
- $k$:波数・・・空間(位置・場所)を移動したときの波の振動の多さ
- $\phi$:初期位相・・・時間と場所を固定したときの波のピーク位置
下のアニメーショングラフで、4つのパラメーターを操作できます。各パラメーターが及ぼす波の挙動がわかると思います。(クリックしてから読み込みまで少し時間がかかることがあります)
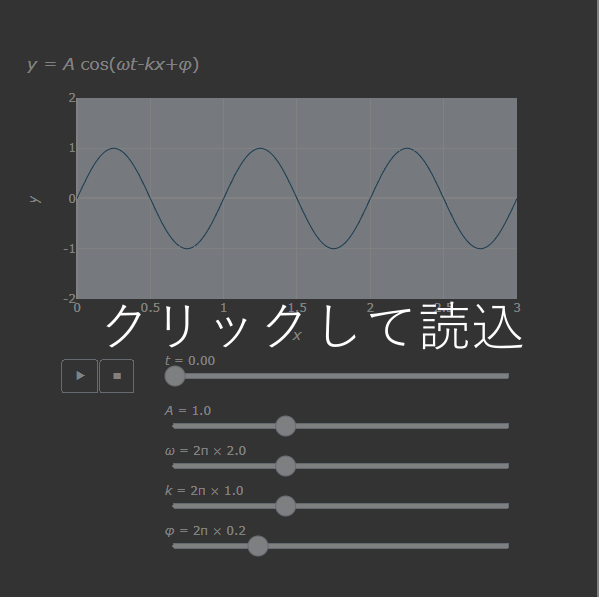
ここで $t$ :時間、$x$ :位置を示しており、上記の4つのパラメーター( $A$, $\omega$, $k$, $\phi$)が波を特徴づけるパラメーターとなります。 物理学では時間と空間(位置・場所)の2つの次元を取り扱うことが多いため、上式のような形式になりますが、信号処理などで位置の次元を必要とせず時間のみを変数とする場合には位置に関する項 $kx$ が消えた
$$A \cos(\omega t+\phi)$$
の形で利用することも多いです。オシロスコープで観測する波も時間のみに依存した波ですね。
時間に関するパラメーター $\omega$ や空間に関するパラメーター $k$ については、下式のように他にも多くの表示方法があり混乱しやすいですが、同じ特徴を持つ波を表します。
$$ A \cos(\omega t-kx+\phi) = A\cos(2\pi\nu t-kx+\phi) = A \cos(2\pi\frac{t}{T}-2\pi\frac{x}{\lambda}+\phi)$$
時間および空間軸上での位相パラメーターをそれぞれ後で取り上げます(本ページでは、それぞれ”時間軸上での位相パラメーター”、”空間軸上での位相パラメーター”と呼ぶことにします)。
Q. cosでなくsinのときがあるが、違いは?
$\cos \theta = \sin(\theta+\pi/4)$ の関係式のように、
$\cos(\omega t-kt+\phi)$$=\sin(\omega t-kt+\phi+\pi/4)$ = $\sin(\omega t-kt+\phi’)$となり($\phi’ \equiv \phi+\pi/4$)、sinとcosは初期位相が異なるだけです。 本質的にはsin波もcos波も同じなので、どちらを使ってもあまり問題にはなりません。 cos波は偶関数であり、位相の符号が正負で同じとなり扱いやすいのでsinよりcosがよく使われるのだと、個人的に思っています。
時間軸上での位相パラメーター
時間 $t$ にかかる係数は、角周波数の他にも周波数や周期という形でも表すことができ、いずれも時間経過に伴う波の往復回数(場所は固定)を決定するパラメーターとなります。これらのどれか1つが決まっていれば、他の2つにも変換可能です。まとめると下の表の通りになります。
| 名称 | 記号 | 単位 | 説明 | 関係式 |
|---|---|---|---|---|
| 角周波数(角振動数) | $\omega$ | rad s$^{-1}$ | 時間1秒当たりの波のピーク数$\times 2\pi$(ラジアン単位になっている=位相角 | $\omega = 2\pi \nu$, $\omega = 2\pi / T$ |
| 周波数(振動数) | $\nu$, $f$ | s$^{-1}$, Hz | 時間1秒当たりの波のピーク数 | $\nu=\omega / 2\pi$, $\nu =1 / T$ |
| 周期 | $T$ | s | 波のピーク間の時間 | $T=2\pi / \omega$, $T=1 / \nu$ |
空間軸上での位相パラメーター
空間xにかかる係数は、波数の他にも波長という形の場合もあり、いずれも空間を移動したときに伴う波の往復回数(時間は固定)を決定するパラメーターとなります。 これらは1つが決まっていれば、他方にも変換可能です。波数というと、$2\pi$ が掛けてある場合とそうでない場合がありややこしいですが、今回は$2\pi$が掛けてあるものとして話を進めます(両者を扱う時、それぞれ角波数k, 波数k’と呼んで区別することもあります)。まとめると下の表の通りになります。
| 名称 | 記号 | 単位 | 説明 | 関係式 |
|---|---|---|---|---|
| 波数(角波数) | $k$ | rad$^ | 空間1m当たりの波のピーク数$\times 2\pi$(ラジアン単位になっている=位相角) | $k = 2\pi k’$, $k = 2\pi / \lambda$ |
| (波数) | $k$, ($k’$) | m$^{-1}$ | 空間1m当たりの波のピーク数 | $k’ = k / 2\pi$, $k’ = 1/\lambda$ |
| 波長 | $\lambda$ | m | 波のピーク間の距離 | $\lambda=2\pi / k$, $\lambda=1 / k’$ |
2次元以上の空間軸上での位相パラメーター:波数ベクトル
空間を表す変数が $x$だけのときのように、扱う空間が1次元のときは上記のように空間軸上での位相パラメーターはすべてスカラーになります。 しかし現実の空間は3次元であるように、多次元空間を扱う場合も少なくありません。このときは、空間軸上での位相パラメーターである波数 $k$はベクトルとして扱われ、波数ベクトルと呼ばれます。
- 1次元空間 $x$ の波:$A \cos(\omega t-kt+\phi)$
- 2次元空間 $\bm{r}=(x,y)$ の波:$A \cos(\omega t-\bm{k\cdot r}+\phi)=A\cos(\omega t-(k_xx+k_yy)+\phi)$
- 波数ベクトル:$\bm{k}=(k_x, k_y)$
波数ベクトルの向きは、空間的に並んでいる同位相の面(等位相面)に対して垂直な方向を示しています(下図)。 このとき、波は平面が進んでいるように表現されるため平面波と呼ばれます。
下のアニメーショングラフで、2次元空間での波の角周波数と波数ベクトルの値を変えることができます。波数ベクトルと波の関係がイメージできるのではないかと思います。(クリックしてから読み込まれるまで時間が少しかかります)

時間軸上・空間軸上の位相パラメーターを結びつけるパラメーター”速度”
時間軸上での位相パラメーターと空間軸上の位相パラメーターとを結びつけるものが”速度 $v$ [m/s]”であり、以下のような関係式になります。
$v = \nu\lambda$ :(1秒間の振動回数)×(ピーク間距離)
$\ \ =\omega/k$ :($2\pi \times$ 1秒間の振動回数)×($2\pi \times$ ピーク間距離)
$\ \ = \lambda/T$ :(ピーク間距離)÷(ピーク間の時間)
つまり波の速度が分かっているのであれば、時間軸上での位相パラメーターから空間軸上での位相パラメーターがわかる、またその逆も然り、ということです。
このように速度の値を使って、時間と空間の位相パラメーター間の変換が容易に行えるのは、速度が時間・空間の位相パラメーターに依存せず常に一定の場合のみです。たとえば真空中での電磁波の場合が該当し、
光速:$c = \omega/k$
の関係があり、光の速度は定数cつまり一定の値であるとして扱うことができます。 一方で、速度が時間・空間の位相パラメーターに依存して変化するような場合は、定数ではなくなるのでもっと複雑になります。
波の速度が時間軸上・空間軸上での位相パラメーターに依存するとき:分散関係
速度が時間・空間軸上での位相パラメーターによって変化するときは、「その系に分散がある」と言い、時間軸上の位相パラメーターと空間軸上での位相パラメーターとを結びつける関係を「分散関係」と言います。 たとえば、物質中を伝搬する電磁波は時間軸上での位相パラメーターによって伝搬する速度が異なるため、速度は常に一定ではなく、以下のような分散関係を持ちます。
$$\displaystyle v(\omega)=\frac{\omega}{k}$$
ここで速度 $v$ に$(\omega)$がついているのは、物質中では波の速度が角周波数 $\omega$に依存して変化することを示しています。 物質の屈折率 $n(\omega)$ というのは、物質中での光(電磁波)の速度 $v(\omega)$と真空中での速度 $c$との比を意味し、物質の屈折率は波長によって変わる(分散を持つ)ということがわかります。
$$\displaystyle n(\omega)=\frac{c}{v(\omega)}$$
ちなみに物質(媒質)が変わっても電磁波の時間軸上での位相パラメーターは変化せず、空間軸上での位相パラメーターと速度が変化します。 分散についてはこちらの記事でも扱っています。
複素数表示
コサイン波と複素数の関係
ここまで波を三角関数の1つであるコサインを使って示してきましたが、複素数を使って表現できます。 オイラーの公式($e^{i\theta} = \cos \theta + i\sin\theta$)を使うと、$\cos \theta = Re[e^{i\theta}]$と表せる($Re[]$: 実部を意味する)ように、実数表示:$A \cos(\omega t -kx + \phi)$ から複素数表示:$Re[A\ e^{i(\omega t -kx +\phi)}]$に変換できます。 複素数表示では、コサイン関数の位相に含まれる変数がべき指数の形になっており、波を特徴づける4つのパラメーター (振幅、時間軸上での位相パラメーター、空間軸上での位相パラメーター、初期位相) を指数の積の形で分離できます。 これが複素数表示のメリットで、掛け算(割り算)を行うだけで波を特徴づける4つのパラメーターを独立に操作することができるようになります。
厳密でない表記と注意点
複素数表示をする時に、$Re[]$を含まない$\cos \theta = e^{i\theta}$という関係式が用いられることもあります。 つまり $A \cos(\omega t -kx + \phi)$を $A\ e^{i(\omega t -kx +\phi)}$ という簡略化した形に変換するということです。
厳密には正しい関係式ではありませんが、線形の演算(微分や積分など)を行うだけであれば問題にはなりません。しかし、積やべき乗を含む演算を行うときには、等号が成り立たないので注意が必要です。
厳密でない複素数表示が問題になる例
たとえば2つの波同士で掛け算を行うときに問題が起こります。 ここでは簡易化するために、波が時間のみに依存し、空間に関しては無視($kx=0$)するとします。 2つの波は実数表示で $A_1 \cos(\omega t+\phi_1)$と $A_2 \cos(\omega t+\phi_2)$ で表すことができ、これらの積は
$$\displaystyle A_1 \cos(\omega t + \phi_1) \times A_2 \cos(\omega t + \phi_2) = \frac{A_1 A_2}{2}[\cos(2\omega t+\phi_1 + \phi_2) + \cos(\phi_1 – \phi_2)]$$ となります。
一方、厳密ではない複素数表示の形で2つの波を掛け合わせると
$$\displaystyle A_1\ e^{i(\omega t +\phi_1)} \times A_2\ e^{i(\omega t +\phi_2)} = A_1 A_2\ e^{i(2\omega t + \phi_1 + \phi_2)}$$
となり、積の後に $\cos \theta = e^{i\theta}$の関係式を用いて実数表示に変換しようとしても、全体にかかっている1/2の係数と $\cos(\phi_1-\phi_2)$ の項が抜け落ちてしまっています。 つまり、
$$\displaystyle A_1 \cos(\omega t + \phi_1) \times A_2 \cos(\omega t + \phi_2) \neq A_1\ e^{i(\omega t +\phi_1)} \times A_2\ e^{i(\omega t +\phi_2)}$$
となり、積を含む演算を行うときに厳密でない複素数表示は使えないということがわかります。
まとめ
物理的な波を特徴づけるパラメーターには、以下の4つがあります。
- 振幅:$A$
- 角周波数、 周波数、 周期(時間軸上での位相パラメーター):$\omega$,$\nu$, $T$
- 波数、 波長(空間軸上での位相パラメーター):$k$, $\lambda$
- 初期位相:$\phi$
波の時間パラメーターと空間パラメーターは、速度によってお互いに変換できます。
また波はコサイン関数による実数表示によって表現できますが、数学的に扱いやすい複素数表示でも表現できます。 ただし、$\cos \theta = e^{i\theta}$という簡易的な形に変換する関係式は厳密には成り立たないので、扱う時には注意が必要です。
本記事では、角周波数や波数が1成分のときの単色波のみを扱いましたが、こちらの記事では複数の成分を足し合わせた合成波を取り扱っています。