【動くグラフ】群速度・位相速度と群速度分散によるパルス広がり

前の記事では、周波数と波数が1成分のみの波（単色波）を取り扱いましたが、今回はさまざまな角周波数と波数を持つ波の合成波について考えていきます。そのときに出てくる”分散”について、ここで取り上げたいと思います。

位相速度と群速度

二つの波の合成波

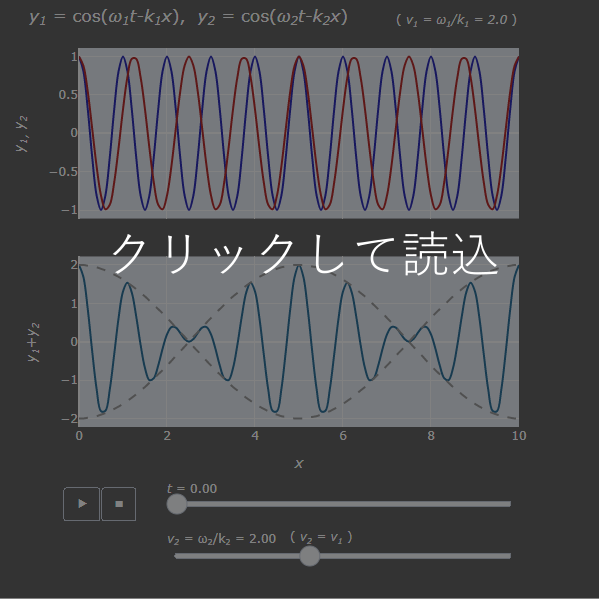
角周波数、波数の異なる2つのコサイン波（orサイン波）を考えます。この2つを足し合わせた合成波は、包絡線が周期的に増減した波になります。微妙に異なる音を混ぜると、うなりとなって聞こえてくるのはこのためです。 周期的な包絡線のことを波束 (wave packet) と呼び、この移動速度のことを群速度 $v_g$ (group velocity) と呼びます。 波束（包絡線）内の細かい波の移動速度の方は位相速度 $v_p$ (phase velocity) と呼びます。(Fig.1)

なぜこのような合成波になるかというと、三角関数の和積の公式を使うとわかります。

角周波数と波数を使った表現に和積の公式を用いると $$\displaystyle \cos(\omega_1 t-k_1 x)+\cos(\omega_2 t -k_2 x) = 2 \cos\left(\frac{\omega_1-\omega_2}{2}-\frac{k_1-k_2}{2} \right)\cos\left(\frac{\omega_1+\omega_2}{2}-\frac{k_1+k_2}{2} \right)$$

となり、以下の2つの積の形になります（Fig.1）。

• $\omega_1-\omega_2$（$k_1-k_2$）を含む角周波数（波数）の小さいコサイン：波束、包絡線
• $\omega_1+\omega_2$（$k_1+k_2$）を含む角周波数（波数）の大きいコサイン：波束内の細かい波

波の速度 $v$ は、角周波数 $\omega$ と波数 $k$ の比で表され

$$v=\omega/k$$

であることから、波束内の細かい波と波束のそれぞれの角周波数と波数から速度を表現すると

• 群速度（波束の速度）：$v_g=(\omega_1-\omega_2)/(k_1-k_2)=(\Delta \omega)/(\Delta k)$
• 位相速度（波束内の細かい波の速度）：$v_p=(\omega_1+\omega_2)/(k_1+k_2) = \omega / k$ になります。

波長分散：位相速度と群速度が異なる条件

波長分散とは

波の波長が変わるとその速度が変わる現象のことを波長分散といいます。 こちらでも扱っていますが、 波の”速度”は”時間軸上での位相パラメーター”と”空間軸上での位相パラメーター”間を結びつけるものになります（Fig.2）。分散がないときは、”時間軸上での位相パラメーター”と”空間軸上での位相パラメーター”の比が一定、つまり速度が一定になります。一方で分散があるときは速度一定にならず、このときの角周波数\omegaと波数kの関係を分散関係と言ったりします。

ここでの時間軸上、空間軸上での位相パラメーターというのは

• 時間軸上での位相パラメーター：角周波数 $\omega$、周波数 $\nu$、周期$T$
• 空間軸上での位相パラメーター：波数$k$、波長$\lambda$

として、勝手に名付けたものです。

時間・空間軸上での位相パラメーターは可換の関係にあるので 「波長分散がある＝波長 $\lambda$, 波数 $k$ によって速度が異なる＝角周波数 $\omega$, 周波数$\nu$, 周期 $T$ によって速度が異なる」 ということになります。（詳しくはこちらの記事参照）。

波長分散によって起こる現象

波長分散があるとき、2つの波によってつくられる合成波の位相速度と群速度に差が生じるということが起こります。 下のアニメーショングラフで合成波の元になる波の速度を変えることができますが、合成前の2つの波に速度差がある（$v_1 \neq v_2$, つまり波長分散がある）とき、位相速度と群速度にずれがあることを確認できると思います（クリックしてから読み込みまで少し時間がかかることがあります）。

屈折率と群速度・位相速度の数式表現

光のような電磁波は透過する物質（媒質）によって伝搬速度が異なり、真空中以外では波長分散が生じます。プリズムによって色ごとに光が分かれるのは、この波長分散があるためです。 媒質中での伝搬速度（の逆数）は屈折率 $n$ で表され※1、 「波長分散がある＝屈折率 $n$ が波長や角周波数等に依存して変化する」 を意味します。これを数式的に表すと

• $\displaystyle \frac{dn}{d\omega}\neq0$ : 波長分散あり
• $\displaystyle\frac{dn}{d\omega}=0$ : 波長分散なし

となり、この関係式を使うと、分散がないとき群速度 $v_g$ と位相速度 $v_p$ が等しくなることを求めることができます (Fig.2)。

• 群速度：$\displaystyle v_g = \frac{\Delta \omega}{\Delta k} -(Δk→0とする)→ \displaystyle \frac{d\omega}{dk} = \frac{c}{n+\omega\frac{dn}{d\omega}}=\frac{c}{n}$

• 位相速度：$\displaystyle v_p = \frac{\omega}{k} = \frac{c}{n}$

群速度 $v_g$ の変換を行っていく過程の最後に $\frac{dn}{d\omega}=0$ を使っています。以上のように、波長分散がないときは群速度と位相速度が同じになりますが、波長分散があるときは等しくなりません。

※1：厳密には、屈折率 $n$ = 真空中の光速度 $c$ と媒質中での速度 $v$ の比

群速度分散：パルスが崩れる条件

ここまではコサイン波2つからなる波を考えてきましたが、ここからはさらに多成分からなる合成波を考えていきます。 波束（= 2成分からなる合成波）を足し合わせていくイメージでしょうか。 このときに、光の短パルスをつくるときなどに出てくるのが群速度分散 (GVD: group velocity dispersion) です。

群速度分散 (GVD) とは

群速度分散というのは、波長（角周波数）によって波束の速度、すなわち群速度 $v_g$ が異なることを言います (Fig.3)。 群速度 $v_g$ は波数kと角周波数 $\omega$ を使って $\frac{1}{v_g}=\frac{dk}{d\omega}$ のように表せることから、

• $\displaystyle \frac{d}{d\omega}\frac{1}{v_g}=\frac{d}{d\omega}\frac{dk}{d\omega}\neq0$ : 群速度分散あり

• $\displaystyle\frac{d}{d\omega} \frac{1}{v_g}=\frac{d}{d\omega}\frac{dk}{d\omega}=0$ : 群速度分散なし

と数式的に表すことができ、この$\frac{d}{d\omega}\frac{1}{dv_g}$の値を群速度分散 (GVD) と呼ぶこともあります。

群速度によって起こる現象

群速度分散があると、他成分の角周波数から構成されるパルスの幅が、パルスの伝番とともに拡大していくということが起こります。

短パルスの形成

短パルスはどうやって作ることができるかというと、初期位相を揃えた波※2を多数足し合わせることによって実現できます（Fig.4）。 足し合わせる角周波数 $\omega$ の成分が多いほどパルス幅を狭くすることができ、その合成波である電場 $E$ の2乗 $E^2$ が短パルスの光強度となります。 足し合わせる角周波数 $\omega$ が多成分ある中で、2つずつのセットで先に合成波（波束）をつくっていくと、「多数の波束を足し合わせることで短パルスをつくることができる」とも考えることができます（Fig.4中央列）。

※2: 一番単純初な条件は期位相 $\phi = 0$ で揃えること

短パルスのパルス幅拡大

短パルスが多数の波束の足し合わせによって形成されていると考えると、それぞれの波束の速度（群速度 $v_g$ ）がパルス幅にとって重要であることがわかります。 ある位置 $x$ で短パルスを形成したとしても、それを構成する波束それぞれの群速度が異なる場合、パルスが伝搬していくにつれて波束の位置がずれていくためパルス幅が広がっていってしまうということ起こります（下のアニメーショングラフで $k(2) \neq 0$ にすると再現できます）。 そのため群速度分散をなくす、ゼロにする、ということが重要になります。

数式的な扱い：テイラー展開による近似

波長分散がある場合、速度つまり屈折率（の逆数）は一定でなく角周波数\omegaに依存して変化し、屈折率は角周波数\omegaの関数となるため、$n(\omega)$と表記することにします。 波数 $k$ と角周波数 $\omega$ の関係式から

$$\displaystyle k=\frac{n(\omega)}{c}\omega$$

ですが、この右辺全体が角周波数 $\omega$ の関数であることから、角周波数 $\omega$ の関数として $\omega _0$ の周りでテイラー展開をして近似できます（$\omega_0$ : $\omega$ の平均値）。 短パルス化するために多くの角周波数 $\omega$成分を足し合わせ、角周波数 $\omega$ の範囲を広げて、$\omega_0$ からより離れた $\omega$ を考慮する必要があるときには、より高次の項まで考える必要があります。

テイラー展開した後の各項の係数はそれぞれ以下のように対応しています（Fig.5）。

各項のパルスへの影響

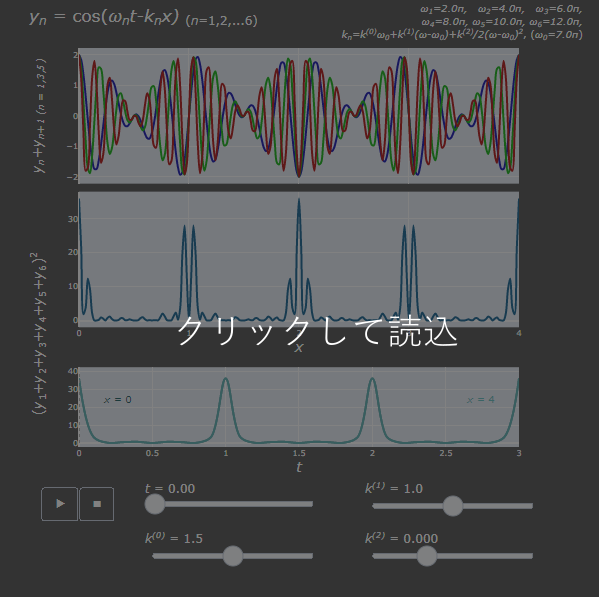
上のアニメーショングラフで、6成分の波によって構成されるパルスの変化を確認できます（クリックしてから読み込みまで少し時間がかかることがあります）。グラフ内では

• 上段：2成分ごとに足し合わせた合成波（波束）
• 中断：6成分すべて足し合わせた合成波の強度（横軸：位置 $x$ ）
• 下段：6成分すべて足し合わせた合成波の強度（横軸：時間 $t$ ）

を表しています。6成分の角周波数 $\omega$ を固定し、それぞれの波数kをテイラー展開近似した関係式によって計算しています。 2次の項を変えたときのみ、パルス幅が変わる（グラフ下段）ことがわかるかと思います。

用語に関する注意点

群速度分散とGVDパラメーター

本記事では、波数kをテイラー展開した2次の項

$$\displaystyle k^{(2)} = \frac{d}{d\omega}\frac{1}{v_g}$$

が群速度分散であるとして書いてきましたが、波数 $k$ のことを伝搬定数 $\beta$ と呼び、これをテイラー展開した2次の項

$$\displaystyle \beta_2 = \frac{d}{d\omega}\frac{1}{v_g}$$

を群速度分散と書いてあることもあります（つまり $k^{(2)}=\beta_2$ に対応）。

また光ファイバーの特性としてよく用いられるのは、（角周波数 $\omega $ でなく）波長 $\lambda$ をもとに群速度分散を表した群速度分散 (GVD) パラメーター $D$ を使うことが多いです。群速度分散パラメーター $D$ と群速度分散 $\beta_2$ の関係は、

$$\displaystyle D=\frac{d}{d\lambda}\frac{1}{v_g} = \frac{d\beta_1}{d\lambda}=-\frac{2\pi c}{\lambda^2}\beta_2$$

で（$\beta_1$: 伝搬定数 $\beta$ のテイラー展開近似の1次の項）、単位の次元が異なります。

群速度分散と群速度分散パラメーター $D$

• 群速度分散：$\beta_2, k^{(2)}$ [ps/(nm・km)]
• 群速度分散パラメーター：$D$ [ps2/km]

群速度分散パラメーターDのことを「群速度分散」「波長分散」と呼ぶ場合もあるので、どれを意味しているのか間違えないようにしたいですね。

正常分散と異常分散

ある媒質が分散を持つとき、長波長の波の方が短波長の波より速く伝搬するとき、そのときの分散を正常分散と呼びます。逆に短波長の波の方が速いときの分散を異常分散と呼びます。 この正常分散・異常分散の区別は、単色波（角周波数が1成分）の速度に関する波長分散に対するものだけでなく、群速度分散に対しても使われます。 そのため正常分散・異常分散と言っても、どちらに対しての分散に関して言っているのか判断する必要があります。

単色波の速度に関する波長分散の区別

	通常分散	異常分散
単色波の速度	長波長 > 短波長（角周波数が小のとき > 大のとき）	長波長 < 短波長 （角周波数が小のとき < 大のとき）
群速度と位相速度	群速度 > 位相速度	群速度 < 位相速度
屈折率の微分	$\displaystyle \frac{dn}{d\omega} > 0$	$\displaystyle \frac{dn}{d\omega} < 0$

群速度分散の区別

	通常分散	異常分散
群速度 $v_g$	長波長 > 短波長	長波長 < 短波長
群速度分散 $\beta_2 (k^{(2)})$ [ps/(nm・km)]	$\displaystyle \frac{d}{d\omega}\frac{1}{v_g} > 0$	$\displaystyle \frac{d}{d\omega}\frac{1}{v_g} < 0$
群速度分散パラメーター $D$ [ps2/km]	$D$ < 0	$D$ >0

まとめ

• 成分の波（単色波）：
  • 角周波数 $\omega$ と波数 $k$ の比によって速度 $v$（屈折率$n$ の逆数）が決まる
• 2成分の波（波束）：
  • 波束の速度＝群速度 $\left( v_g = \frac{\Delta \omega}{\Delta k} \right)$
  • 波長分散（2成分の速度差）によって、位相速度 $v_p \neq$ 群速度 $v_g$ になる
• 多成分の波（パルス）：
  • 多数の波（波束）を足し合わせて短パルス形成
  • 波束間に速度差がある＝群速度分散があるとパルス幅拡大
  • 波数 $k$ を角周波数 $\omega$ の関数としてテイラー展開近似すると2次の項 $\displaystyle\displaystyle \frac{d}{d\omega}\frac{1}{v_g}$ が群速度分散に相当