偏光(偏波)をインタラクティブなグラフで描画
投稿日:2020年3月11日 更新日:
内容
- 偏光(偏波)をインタラクティブなグラフで表現
- 強度比と位相差による偏波の変化について
動機
Pythonにはいろいろなグラフ作成ライブラリがありますが、中でもインタラクティブな(グリグリ動かせる)グラフが作れるplotlyというライブラリがあります。
興味が湧き、前回の記事で扱ったような偏光の様子がみられれぱ、より理解が深まるのでは、ということでplotlyを使って偏光を表すグラフを作ってみました。
インタラクティブなグラフ
plotlyを使ったグラフ
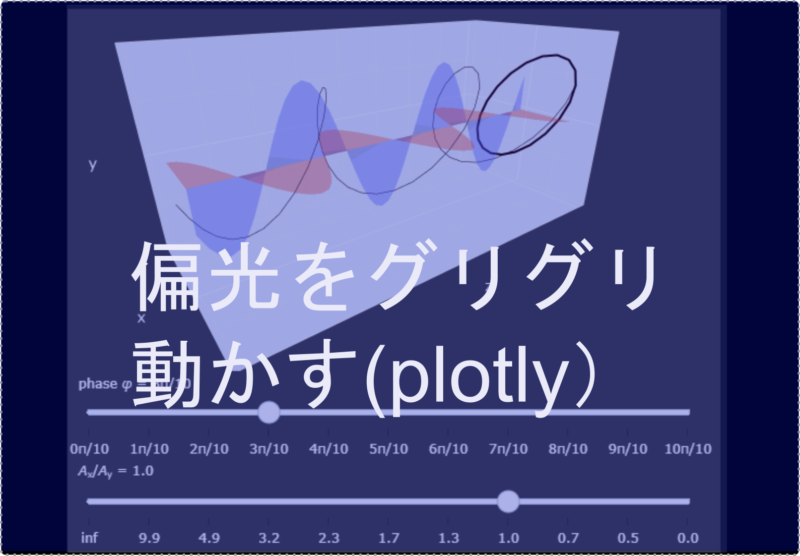
プロットしているものは以下の通りです(ここでは複素数は用いていません)。
- 青メッシュ: x方向の波 $E_x=A_x \cos(2\pi z)$
- 赤メッシュ : y方向の波 $E_y=A_y \cos(2\pi z+\phi)$
- 黒線(細): $E_x$と$E_y$によって作られる偏光
- 黒線(太):$E_x$と$E_y$によって作られる偏光($x-y$平面上にプロット)
($A_x$ ($A_y$): $E_x$ ($E_y$)の強度, $\phi$: $E_x$と$E_y$の位相差)
※ $A_x^2+A_y^2=1$を満たす。
グラフの操作
- 左クリックしながらマウス移動で、角度変更
- 右クリックしながらマウス移動で、平行移動
- マウスホイールで、拡大縮小
となっています。右上の方にあるアイコンでカメラ位置をリセットしたりできます。またグラフの下にある2つのスライダーで縦・横方向の波の位相差$\phi$と強度比$A_x/A_y$が変えられます。
ソースコード(Python)
【表示する】
# %%
import plotly.graph_objects as go
import plotly.offline as py
import numpy as np
py.init_notebook_mode(connected=True)
#%%
def makeMesh(x):
x=np.hstack((0,x,99))
elem0=np.abs(x)<1e-10
elenum0=np.where(elem0)[0]
u0=elenum0[np.cumsum(elem0)-1]
u=(np.delete(u0,elenum0))[:-1]
v0=np.arange(len(u0))
v=(np.delete(v0,(elenum0)))[:-1]
w=v+1
return u,v,w
#%%
z=np.pi*np.linspace(0,5,51)
z2=np.hstack((0,z,z[-1]))
fig=go.Figure()
#%%
x=np.cos(z)
ux,vx,wx=makeMesh(x)
x=np.hstack((0,x,0))
#%%
phi = np.pi/2
y=np.cos(z+phi)
uy,vy,wy=makeMesh(y)
y=np.hstack((0,y,0))
#%%
for j in range(11):
Ax=j/10. #Ax:0-1
x2=Ax*x
Ay=np.sqrt(1-np.square(Ax)) #Ay=sqrt(1-Ay^2)
y2=Ay*y
fig.add_trace(
go.Mesh3d(
x=0*z2, y=y2, z=z2,
i=uy, j=vy, k=wy,
opacity=0.4,
scene = 'scene1',
visible = False,
name = "<i>E</i><sub>Y</sub>",
hoverinfo="name",
))
fig.add_trace(
go.Mesh3d(
x=x2, y=0*z2, z=z2,
i=ux, j=vx, k=wx,
opacity=0.4,
scene='scene1',
visible=False,
name = "<i>E</i><sub>X</sub>",
hoverinfo="name",
))
fig.add_trace(
go.Scatter3d(
x=x2[1:-1], y=y2[1:-1], z=z2[1:-1],
mode='lines',
line=dict(
color='#1f0000',
width=1
),
scene='scene1',
visible=False,
name = "<i>E</i>",
hoverinfo="name",
))
fig.add_trace(
go.Scatter3d(
x=x2[1:-1], y=y2[1:-1], z=z2[1:-1]*0.0,
mode='lines',
line=dict(
color='#1f0000',
width=4
),
scene='scene1',
visible=False,
name = "<i>E</i> at x-y plane",
hoverinfo="name",
))
#%%
fig.data[28].visible = True
fig.data[29].visible = True
fig.data[30].visible = True
fig.data[31].visible = True
fignum=4 # number of trace
steps1 = []
#%%
for i in np.arange(0, 11, 1):
phi = np.pi*i/10
y=np.cos(z+phi)
uy,vy,wy=makeMesh(y)
y=np.hstack((0,y,0))
step1 = dict(
method="restyle",
label='%dπ/10' % i,
args=[{"y": [0*z2]*len(fig.data),
"i": [uy,ux,"",""]*int(len(fig.data)/fignum),
"j": [vy,vx,"",""]*int(len(fig.data)/fignum),
"k": [wy,wx,"",""]*int(len(fig.data)/fignum),
}]
)
for j in range(11):
Ay=np.sqrt(1-np.square(j/10.))
y2= Ay*y
step1["args"][0]["y"][fignum*j] = y2
step1["args"][0]["y"][fignum*j+2] = y2[1:-1]
step1["args"][0]["y"][fignum*j+3] = y2[1:-1]
steps1.append(step1)
#%%
steps2 = []
for j in range(int(len(fig.data) / fignum )):
Ax=j/10.,
step2 = dict(
method="restyle",
label="%.1f" % (np.sqrt(1-np.square(Ax))/Ax)[0],
args=["visible", [False] * len(fig.data)],
)
step2["args"][1][fignum*j] = True
step2["args"][1][fignum*j+1] = True
step2["args"][1][fignum*j+2] = True
step2["args"][1][fignum*j+3] = True
steps2.append(step2)
#%%
sliders = [dict(
active=5,
currentvalue={"prefix": "phase <i>φ</i> = "},
pad={"t": 0, "r":20, "l":10},
steps=steps1
),dict(
active=7,
currentvalue={"prefix": "<i>A</i><sub>x</sub>/<i>A</i><sub>y</sub> = "},
pad={"t": 80, "r":20, "l":10,"b":10},
steps=steps2
)]
#%%
camera = dict(
up=dict(x=0, y=0.5, z=0),
center=dict(x=0, y=-0.2, z=0),
eye=dict(x=1.2, y=0.5, z=0.9),
)
fig['layout'].update(
scene_camera=camera,
autosize=True,
margin=dict(l=0.0, r=0.0, b=0.0, t=0),
showlegend=False,
sliders=sliders,
paper_bgcolor='#414141',
plot_bgcolor = '#ffe3e3',
font = dict(color="#fff"),
height=500, width=600)
fig['layout']['scene1'].update(aspectratio=dict(x=0.7,y=0.7,z=1.5),
xaxis=dict(color="#fff" ,linecolor="#fff" ,gridcolor="#eee" ,range=[-1.,1.], showticklabels=False),
yaxis=dict(color="#fff" ,linecolor="#fff" ,gridcolor="#eee" ,range=[-1.,1.], showticklabels=False),
zaxis=dict(color="#fff" ,linecolor="#fff" ,gridcolor="#eee" ,showticklabels=False))
py.iplot(fig)
偏光の条件
直線偏光
$\phi=0$ or $\pi$のとき、すなわち$E_x$と$E_y$の波の山(谷)がそろっているときは、直線偏光となります。
このとき、$A_x/A_y$の値を変えると直線偏光の傾きが変化します。また$A_x/A_y=0$ or $\infty$のときは、
$\phi$の値に関わらず直線偏光になります($A_x$, $A_y$のどちらかが0、つまり$E_x$, $E_y$のどちらかの成分が全くないという条件ですので)。
円偏光
$\phi=\pi/2$かつ$A_x/A_y=1$のときは、円偏光となります。波の山と谷のちょうど中間で、もう片方の波の山(谷)が来るタイミングとなるように$E_x$と$E_y$の位相がずれ、尚且つ縦・横の成分の大きさが等しい、という限定的な条件でのみ円偏光がみられるということですね。それ以外の条件では、直線偏光になる条件を除いて、楕円偏光になります。
まとめ
Pythonのplotlyを使って偏光を表したプロットを作成しました。横(x)方向と縦方向(y)の波の強度比を変えると、直線偏光の傾きが変わることや、位相差を操作することで円偏光が作り出せることが視覚的にわかると思います。
plotly面白いですが、なかなか思い通りに行かないこともありますね。スライダーで2つのパラメータ操作や、メッシュの生成に苦労しました…。